题目内容
15. 如图所示,线圈内有理想边界的磁场,开始时磁场的磁感应强度为B0.当磁场均匀减小时,有一带电微粒静止于平行板(两板水平放置)电容器中间,若线圈的匝数为n,平行板电容器的板间距离为d,粒子的质量为m,带电荷量为q.(设线圈的半径为r)求:
如图所示,线圈内有理想边界的磁场,开始时磁场的磁感应强度为B0.当磁场均匀减小时,有一带电微粒静止于平行板(两板水平放置)电容器中间,若线圈的匝数为n,平行板电容器的板间距离为d,粒子的质量为m,带电荷量为q.(设线圈的半径为r)求:(1)开始时穿过线圈平面的磁通量的大小.
(2)处于平行板电容器间的粒子的带电性质.
(3)磁感应强度的变化率.
分析 (1)根据磁通理定义,即可求解;
(2)由楞次定律判断出感应电动势的方向,判断出极板间电场的方向,然后判断微粒的电性;
(3)由平衡条件求出极板间的电场强度,求出极板间的电势差,然后由法拉第电磁感应定律求出磁感应强度的变化率.
解答 解:(1)根据磁通理定义,∅=B0•S=B0•πr2;
(2)由图示可知,磁场垂直与纸面向里,磁感应强度减小,穿过线圈的磁通量减小,
由楞次定律可知,平行板电容器的上极板电势低,下极板电势高,板间存在向上的电场,
微粒受到竖直向下的重力而静止,因此微粒受到的电场力向上,电场力方向与场强方向相同,微粒带正电;
(3)对微粒,由平衡条件得:mg=q$\frac{E}{d}$,
感应电动势:E=$\frac{mgd}{q}$,
由法拉第电磁感应定律得:E=$\frac{△∅}{△t}$=S$\frac{△B}{△t}$,
解得:$\frac{△B}{△t}$=$\frac{mgd}{π{r}^{2}q}$;
答:(1)开始时穿过线圈平面的磁通量的大小B0•πr2.
(2)处于平行板电容器间的粒子的带正电.
(3)磁感应强度的变化率$\frac{mgd}{π{r}^{2}q}$.
点评 正电荷所受电场力方向与场强方向相同,负电荷所受电场力方向与场强方向相反;应用楞次定律判断出极板间场强的方向即可判断出微粒的电性.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
6.在x轴上有两个点电荷,一个带正电荷Q1,一个带负电荷Q2,Q1=2Q2,用E1和E2,分别表示两个电荷所产生场强的大小,则在x轴上( )
| A. | E1=E2之点只有一处,该处合场强为零 | |
| B. | E1=E2之点只有两处,一处合场强为零,另一处合场强为2E2 | |
| C. | E1=E2之点只有三处,其中两处合场强为零,另一处合场强为2E2 | |
| D. | E1=E2之点只有三处,其中两处合场强为零,另两处合场强为2E2 |
10. 如图所示,木块放在木板上,木板放在水平面上,且木板的左端用铰链固定.现将其右端缓慢地抬高,当木块刚好开始沿木板滑动时,测出当时木板和水平面间的夹角为θ.下列说法正确的是( )
如图所示,木块放在木板上,木板放在水平面上,且木板的左端用铰链固定.现将其右端缓慢地抬高,当木块刚好开始沿木板滑动时,测出当时木板和水平面间的夹角为θ.下列说法正确的是( )
 如图所示,木块放在木板上,木板放在水平面上,且木板的左端用铰链固定.现将其右端缓慢地抬高,当木块刚好开始沿木板滑动时,测出当时木板和水平面间的夹角为θ.下列说法正确的是( )
如图所示,木块放在木板上,木板放在水平面上,且木板的左端用铰链固定.现将其右端缓慢地抬高,当木块刚好开始沿木板滑动时,测出当时木板和水平面间的夹角为θ.下列说法正确的是( )| A. | 在木块开始滑动前,木块所受的摩擦力一直在增大 | |
| B. | 在木块开始滑动前,木块所受的摩擦一直在减小 | |
| C. | 测得的动摩擦因数μ=tanθ | |
| D. | 测得的动摩擦因数μ=sinθ |
4.下列关于功的说法中正确的是( )
| A. | 由于功有正负,所以功是矢量 | |
| B. | 计算式W=FScosα中,F是力的大小,S是位移的大小,α是力F和位移S方向上的夹角 | |
| C. | 合力对物体做的功,等于各分力做功的矢量和 | |
| D. | 摩擦力做功,一定是负功,起到阻碍作用 |
 如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求:
如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求:



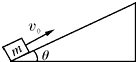 如图所示,质量为m=2Kg的木块(可视为质点)沿倾角为θ=53°的足够长的固定斜面以初速度v0=11m/s向上运动,已知木块与斜面间的动摩擦因数为μ=0.5.(g=10/s2)求:
如图所示,质量为m=2Kg的木块(可视为质点)沿倾角为θ=53°的足够长的固定斜面以初速度v0=11m/s向上运动,已知木块与斜面间的动摩擦因数为μ=0.5.(g=10/s2)求: