��Ŀ����
6����ͼ1��ʾ����һС����б�涥���ɾ�ֹ�ͷţ�С��龭��A����B�㣬С�������AB֮��ľ����С��龭��AB���õ�ʱ�䣬�ı�A��λ�ã��������AB��༰����AB���õ�ʱ��t��С��������AB��ƽ���ٶ�$\overline{v}$�뾭��ʱ��t��ͼ������˵����ȷ���ǣ�������
| A�� | ��ͼ������С��鵽��B����ٶ� | |
| B�� | ��ͼ���֪С������ȼ���ֱ���˶� | |
| C�� | ͼ�ߺ�t����Χ���������б��ij��� | |
| D�� | ��ͼ���֪С����˶��ļ��ٶȴ�С����$\frac{v}{2{t}_{0}}$ |
���� ������б�����ȼ����»�������ƽ���ٶȹ�ʽ$\overline{v}$=$\frac{{v}_{0}+v}{2}$��B����ٶȣ���ͼ�����ٶ�ʱ��ͼ�����������ʾλ�ƣ�
��� �⣺A����ͼ֪�������A�˶���B��ʱ��Ϊt0��ƽ���ٶ�Ϊ$\overline{v}$=$\frac{v}{2}$�������嵽��B����ٶ�ΪvB��
б��ij���L=$\overline{v}$t0=$\frac{v}{2}{t}_{0}$����L=$\frac{0+{v}_{B}}{2}{t}_{0}$�ã�vB=v�����Կ����С��鵽��B����ٶȣ���A��ȷ��
B����ͼ�����ٶ�ʱ��ͼ����ͼ����ȷ��������ȼ���ֱ���˶������Ӿ�ֹ��ʼ���������ȼ���ֱ���˶�����B����
C����ͼ�����ٶ�ʱ��ͼ��ͼ������������Χ���������ʾλ�ƣ���֪ͼ�ߺ�t����Χ�����������б��ij��ȣ���C����
D����L=$\frac{1}{2}a{t}_{0}^{2}$����a=$\frac{2L}{{t}_{0}^{2}}$=$\frac{2��\frac{v}{2}{t}_{0}}{{t}_{0}^{2}}$=$\frac{v}{{t}_{0}}$����D����
��ѡ��A��
���� �������Ĺؼ��Ƕ�������A�˶���B��ʱ���ƽ���ٶȣ�Ҫע��ƽ���ٶ�ͼ�����ٶ�ͼ������𣬲��ܵ���һ���£�

��ϰ��ϵ�д�
�����Ŀ
1��������ϵʽ������ӳ��������֮���������ϵ��Ҳȷ����������֮��ĵ�λ��ϵ��������������λ��m���ף���s���룩��J��������W���ߣ���C���⣩��A������������ŷ����T���أ�����������ϳɵĵ�λ���ѹ��λV��������Ч���ǣ�������
| A�� | J/A | B�� | W/�� | C�� | T•m2/s | D�� | T•A•m |
18�� ��ͼ��ʾ�������ѹ��ԭ��Ȧ�����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������10��1������Ȧ��·��R0Ϊ��ֵ���裬R�ǹ������裨����ֵ�����ǿ�ȵ��������С����ͼ�е����Ϊ������������˵������ȷ���ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ�����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������10��1������Ȧ��·��R0Ϊ��ֵ���裬R�ǹ������裨����ֵ�����ǿ�ȵ��������С����ͼ�е����Ϊ������������˵������ȷ���ǣ�������
 ��ͼ��ʾ�������ѹ��ԭ��Ȧ�����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������10��1������Ȧ��·��R0Ϊ��ֵ���裬R�ǹ������裨����ֵ�����ǿ�ȵ��������С����ͼ�е����Ϊ������������˵������ȷ���ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ�����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������10��1������Ȧ��·��R0Ϊ��ֵ���裬R�ǹ������裨����ֵ�����ǿ�ȵ��������С����ͼ�е����Ϊ������������˵������ȷ���ǣ�������| A�� | ��ѹ�������ѹ��Ƶ��Ϊ5Hz | |
| B�� | ��ѹ��V2��ʾ��Ϊ22$\sqrt{2}$V | |
| C�� | ����R�Ĺ��ǿ������L�䰵 | |
| D�� | ����R�Ĺ��ǿʱ����ѹ��V1��������A1��ʾ�������� |
15��ij�����о�С��Ұ�⿼��ʱ����һɽ�壬���������λ�ø߶ȣ���������ʵ�飺��ϸ��˩��Сʯ��ϵ����֦������һ�������ڣ�������Я���ĸ־��߲�����㵽ʯ�����ĵij���L��Ȼ��ʯ������һ��С�Ƕȣ��ɾ�ֹ�ͷţ�ʹ������ֱƽ���ڰڶ����õ����ֱ�����������n��ȫ�����õ�ʱ��t������֪����뾶ΪR����ƽ�洦�������ٶ�Ϊg0�ɴ˿������������λ�õĺ��θ߶�Ϊ��������
| A�� | $\frac{2��n}{Rt}$$\sqrt{\frac{{g}_{0}}{L}}$-R | B�� | $\frac{Rt}{2��n}$$\sqrt{\frac{L}{{g}_{0}}}$-R | C�� | $\frac{2��Rt}{n}$$\sqrt{\frac{L}{{g}_{0}}}$-R | D�� | $\frac{Rt}{2��n}$$\sqrt{\frac{{g}_{0}}{L}}$-R |
16��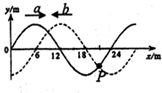 �������Ϊ2cm������24cm�Ͳ���12m/s��г�Შa��b���ֱ���x�����������������t=0ʱ�̵IJ��ֲ���ͼ��ͼ��ʾ��������
�������Ϊ2cm������24cm�Ͳ���12m/s��г�Შa��b���ֱ���x�����������������t=0ʱ�̵IJ��ֲ���ͼ��ͼ��ʾ��������
 �������Ϊ2cm������24cm�Ͳ���12m/s��г�Შa��b���ֱ���x�����������������t=0ʱ�̵IJ��ֲ���ͼ��ͼ��ʾ��������
�������Ϊ2cm������24cm�Ͳ���12m/s��г�Შa��b���ֱ���x�����������������t=0ʱ�̵IJ��ֲ���ͼ��ͼ��ʾ��������| A�� | ͼ��x=15m�����ʵ��Ǽ�ǿ�� | |
| B�� | ͼ��x=21m����P�ʵ㾭ʱ��t=0.75�����ٶ����ֵ | |
| C�� | �����в��������ܷ����������� | |
| D�� | ��������Ҫ�������Ե������������������ϰ���ijߴ�һ�㲻����2cm |


 ���ʺ���̫���⾭�������Сˮ��������γɵģ�̫���⾭��Сˮ�������ijɫ��Ĺ�·��ͼ��ʾ��������������ߺͳ�������ӳ��ߣ����������нǣ�����̫�����Ǹ�ɫ�⣬��ˮ�Բ�ͬɫ�������ʲ�ͬ����Ƶ��Խ�ߣ�������Խ�����ɫ����ˮ���еĴ����ٶ�������Ϲ⾭��Сˮ�����������������ѡ���������=����������
���ʺ���̫���⾭�������Сˮ��������γɵģ�̫���⾭��Сˮ�������ijɫ��Ĺ�·��ͼ��ʾ��������������ߺͳ�������ӳ��ߣ����������нǣ�����̫�����Ǹ�ɫ�⣬��ˮ�Բ�ͬɫ�������ʲ�ͬ����Ƶ��Խ�ߣ�������Խ�����ɫ����ˮ���еĴ����ٶ�������Ϲ⾭��Сˮ�����������������ѡ���������=����������