题目内容
14．
如图所示，斜面体固定在水平地面上，斜面表面是光滑的且足够长．斜面顶端与自然长度为L的轻质弹簧相连，弹簧的另一端连接着物块m，当物块静止时，弹簧的伸长量为△l．压缩弹簧使弹簧长度为$\frac{3}{4}$L时将物块由静止释放，则物块运动过程中，弹簧的最大伸长量为（运动过程中弹簧未超过弹性限度）| A． | $\frac{L}{4}$+2△l | B． | $\frac{L}{4}$+△l | C． | L+2△l | D． | L+△l |
分析 物体平衡时，受重力、支持力和弹簧的弹力，三力平衡，根据平衡条件确定平衡位置；简谐运动具有对称性，先求解出振幅，然后确定最大伸长量；
解答 解：由题，当物块静止时，弹簧的伸长量为△l；根据简谐运动的对称性，压缩弹簧使其长度为$\frac{3}{4}$L时将物块由静止开始释放，故其振幅为：
A=$\frac{1}{4}$L+△l
故其最大伸长量为：A+△l=$\frac{1}{4}$L+2△l
故A正确，BCD错误
故选：A
点评 本题关键是先对滑块受力分析，利用简谐运动的对称性求解弹簧最大伸长量，灵活性就强．
练习册系列答案
相关题目
5．
如图所示，足够长的平行光滑导轨固定在水平面上，电阻忽略不计，其右端连接有两个定值电阻R1、R2，电键S处于断开状态，整个装置处于竖直方向的匀强磁场中．一电阻为R3的导体棒在恒定的水平外力F的作用下在导轨上匀速向左运动，运动中导体棒始终与导轨垂直．现将电键S闭合，下列说法正确的是（ ）
如图所示，足够长的平行光滑导轨固定在水平面上，电阻忽略不计，其右端连接有两个定值电阻R1、R2，电键S处于断开状态，整个装置处于竖直方向的匀强磁场中．一电阻为R3的导体棒在恒定的水平外力F的作用下在导轨上匀速向左运动，运动中导体棒始终与导轨垂直．现将电键S闭合，下列说法正确的是（ ）| A． | 刚闭合S的瞬间，导体棒中的电流不变 | |
| B． | 刚闭合S的瞬问，导体棒两端电压增大 | |
| C． | 闭含S后，导体棒做减速运动直到停止 | |
| D． | 闭合S后，导体棒做减速运动直到再一次匀速运动 |
2．从同一位置以相同的速率把完全相同的甲、乙、丙三个小球分别竖直向上、竖直向下及水平抛出后落到同一水平地面上．不计空气阻力，不考虑小球反弹，则（ ）
| A． | 落地时乙球的动能最大 | B． | 落地时甲球的动能最大 | ||
| C． | 丙球的重力做功的平均功率最小 | D． | 落地时丙球重力的瞬时功率最小 |
9．如图所示，水平传送带的长度L=5m，皮带轮的半径R=0.1m，皮带轮以角速度ω顺时针匀速转动，现有一小物体（视为质点）以水平速度v0从A点滑上传送带，越过B点后做平抛运动，其水平位移为x．保持物体的初速度v0不变，多次改变皮带轮的角速度ω，依次测量水平位移x，得到如图所示的x-ω图象，则下列说法正确的是（ ）
| A． | 当0＜ω＜10rad/s时，物体在AB之间做匀减速直线运动 | |
| B． | 当ω≥30rad/s时，物体在AB之间做匀速直线运动 | |
| C． | B端距地面的高度h=5m | |
| D． | 物体水平初速度为v0=5m/s |
19．
如图甲所示，在光滑水平面上的两个小球发生正碰，小球的质量分别为m1和m2，图乙为它们碰撞前后的x-t图象．已知m1=0.1kg，由此可以判断（ ）
如图甲所示，在光滑水平面上的两个小球发生正碰，小球的质量分别为m1和m2，图乙为它们碰撞前后的x-t图象．已知m1=0.1kg，由此可以判断（ ）| A． | 碰后m2和m1都向右运动 | |
| B． | 碰前m1静止，m2向右运动 | |
| C． | 碰撞过程中系统损失了0.4J的机械能 | |
| D． | 由动量守恒可以算出m2=0.3kg |
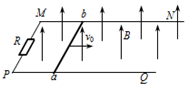如图所示，水平面上有两根足够长的光滑平行金属导轨MN和PQ，两导轨间距为L，电阻均可忽略不计，在M和P之间接有阻值为R的定值电阻．导体杆ab质量为m，电阻为r，并与导轨接触良好．整个装置处于方向竖直向上、磁感应强度为B的匀强磁场中．现给ab杆大小为v0的初速度，使杆向右运动．求：