题目内容
10. 如图所示,两个挨得很近的小球,从斜面上的同一位置O以不同的初速度vA、vB做平抛运动,斜面足够长,在斜面上的落点分别为A、B,空中运动的时间分别为tA、tB,碰撞斜面前瞬间的速度与斜面的夹角分别为α、β,已知OB=2OA.则有( )
如图所示,两个挨得很近的小球,从斜面上的同一位置O以不同的初速度vA、vB做平抛运动,斜面足够长,在斜面上的落点分别为A、B,空中运动的时间分别为tA、tB,碰撞斜面前瞬间的速度与斜面的夹角分别为α、β,已知OB=2OA.则有( )| A. | vA:vB=1:$\sqrt{2}$ | |
| B. | tA:tB=1:2 | |
| C. | α>β | |
| D. | B球离斜面最远的位置在A点的正上方 |
分析 根据竖直位移之比得出平抛运动的时间之比,结合水平位移之比和时间之比求出初速度之比.抓住平抛运动某时刻速度方向与水平方向夹角的正切值是位移方向与水平方向夹角的正切值的2倍,得出α与β的关系.
解答 解:A、由几何关系知,平抛运动的竖直位移之比为1:2,根据t=$\sqrt{\frac{2h}{g}}$知,${t}_{A}:{t}_{B}=1:\sqrt{2}$,根据${v}_{0}=\frac{x}{t}$知,水平位移之比为1:2,则初速度之比vA:vB=1:$\sqrt{2}$,故A正确,B错误.
C、平抛运动某时刻速度方向与水平方向夹角的正切值是位移方向与水平方向夹角的正切值的2倍,以为你两球落在斜面上,位移方向相同,则速度方向相同,可知碰撞斜面前瞬间的速度与斜面的夹角相同,故C错误.
D、当速度方向与斜面平行时,B球离斜面最远,此时有tanθ=$\frac{gt}{{v}_{B}}$,$t=\frac{{v}_{B}tanθ}{g}$,落到底端时,有:tanθ=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{B}t}$=$\frac{gt}{2{v}_{B}}$,解得$t′=\frac{2{v}_{B}tanθ}{g}$,可知B球离斜面最远时,运动时间是总时间的一半,此时水平位移是B球水平位移的一半,即在A点的正上方.故D正确.
故选:AD.
点评 解决本题的关键抓住平抛运动落在斜面上竖直方向上的位移和水平方向上的位移的比值是定值,明确当速度方向与斜面平行时,球离斜面最远,注意几何关系在解题中的应用,难度适中.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15.下列说法正确的是( )
| A. | 奥斯特发现了电流的磁效应并提出了电磁感应定律 | |
| B. | 楞次发现了电流的磁效应,并研究得出了判断感应电流的方向的方法---楞次定律 | |
| C. | 发生多普勒效应时,波源的频率变化了 | |
| D. | “闻其声不见其人”是声波的衍射现象 |
1.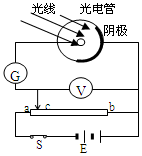 用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )
用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )
 用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )
用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )| A. | 光电子的最大初动能始终为1.05eV | |
| B. | 光电管阴极的逸出功为1.05eV | |
| C. | 电键S断开后,电流表G中有电流流过 | |
| D. | 改用能量为2.5eV的光子照射,移动变阻器的触点c,电流表G中也可能有电流 |
18. 如图所示,一带电小球悬挂在平行板电容器内部,闭合电键S,电容器充电后,细线与竖直方向夹角为α,则下列说法正确的是( )
如图所示,一带电小球悬挂在平行板电容器内部,闭合电键S,电容器充电后,细线与竖直方向夹角为α,则下列说法正确的是( )
 如图所示,一带电小球悬挂在平行板电容器内部,闭合电键S,电容器充电后,细线与竖直方向夹角为α,则下列说法正确的是( )
如图所示,一带电小球悬挂在平行板电容器内部,闭合电键S,电容器充电后,细线与竖直方向夹角为α,则下列说法正确的是( )| A. | 保持电键S闭合,使两极板稍靠近一些,α将增大 | |
| B. | 保持电键S闭合,将滑动变阻器滑片向右移动,α将不变 | |
| C. | 断开电键S,使两极板稍靠近一些,α将减小 | |
| D. | 断开电键S,若将细线烧断,小球将做曲线运动 |
5. 如图所示,在发射地球同步卫星的过程中,卫星首先入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道II,则( )
如图所示,在发射地球同步卫星的过程中,卫星首先入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道II,则( )
 如图所示,在发射地球同步卫星的过程中,卫星首先入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道II,则( )
如图所示,在发射地球同步卫星的过程中,卫星首先入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道II,则( )| A. | 该卫星的发射速度必定大于11.2km/s | |
| B. | 卫星在同步轨道II上的运行速度大于7.9km/s | |
| C. | 卫星在轨道I上经过Q点的速度小于在轨道II上经过Q点的速度 | |
| D. | 卫星在轨道I上的周期大于在轨道II的周期 |
15. 质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )
质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )
 质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )
质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )| A. | 碰撞前两物体动量相同 | |
| B. | 质量m1等于质量m2 | |
| C. | 碰撞后两物体一起做匀速直线运动 | |
| D. | 碰撞前两物体动量大小相等、方向相反 |
4.将能够产生匀强磁场的磁铁安装在火车首节车厢下面,如图(甲)(俯视图)所示,当它经过安放在两铁轨间的线圈时,线圈会产生一个电信号传输给控制中心,已知矩形线圈的长为L1,宽为L2,匝数n,若安装在火车车厢下南的磁铁产生的匀强磁场的宽度大于L2,当火车通过安放在铁轨之间的矩形线圈时,控制中心接收到的线圈两端的电压信号u随时间t变化的关系如图乙所示,不计线圈电阻,据此可知:火车的加速度;和安装在火车首节车厢下面的磁铁产生的匀强磁场宽度( )


| A. | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| B. | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| C. | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| D. | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2+t1) |
5.一汽车在水平地面上以恒定功率P=20kw启动,所受的阻力大小是f=1000N,汽车启动后能达到的最大速度为( )
| A. | 40m/s | B. | 30 m/s | C. | 20 m/s | D. | 10 m/s |
 如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为2$\sqrt{3}$m/s,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求:
如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为2$\sqrt{3}$m/s,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求: