题目内容
8. 如图所示,AB为倾角θ=37°的斜面轨道,轨道的AC部分光滑,CB部分粗糙,BP为圆心角等于143°、半径R=0.5m的竖直光滑圆弧形轨道,两轨道相切于B点,P、O两点在同一竖直线上,轻弹簧一端固定在A点,另-端在斜面上C点处,现有一质量m=2kg的小物块(可视为质点)在B点以初速度v0=3m/s沿斜面向下运动,压缩弹簧到D点时速度为0,已知斜面BC部分长度sBC=1m,sCD=0.2m,小物块与斜面BC部分间的动摩擦因数μ=0.25,sin37°=0.6°,cos37°=0.8,g取10m/s2.试求:
如图所示,AB为倾角θ=37°的斜面轨道,轨道的AC部分光滑,CB部分粗糙,BP为圆心角等于143°、半径R=0.5m的竖直光滑圆弧形轨道,两轨道相切于B点,P、O两点在同一竖直线上,轻弹簧一端固定在A点,另-端在斜面上C点处,现有一质量m=2kg的小物块(可视为质点)在B点以初速度v0=3m/s沿斜面向下运动,压缩弹簧到D点时速度为0,已知斜面BC部分长度sBC=1m,sCD=0.2m,小物块与斜面BC部分间的动摩擦因数μ=0.25,sin37°=0.6°,cos37°=0.8,g取10m/s2.试求:(1)弹簧被压缩到D点时的弹性势能Ep;
(2)小物块在沿轨道运动的过程中,系统产生的热量Q;
(3)若改变小物块在B点向下的初速度vB,使小物块在沿轨道运动的过程中不脱离轨道,求vB的范围.
分析 (1)小物块从B点下滑直到压缩弹簧的过程中,物块的机械能转化为内能和弹簧的弹性势能,根据能量守恒定律列式,求弹性势能Ep;
(2)系统产生的热量Q等于克服摩擦力做功,由功能关系求解.
(3)要使小物块在沿轨道运动的过程中不脱离轨道,物块由弹簧反弹上升的最高点为与O等高的点.对整个过程,运用能量守恒定律列式求解.
解答 解:(1)物块从B到D的过程,由能量守恒定律得
mgsin37°•(sCD+sCD)+$\frac{1}{2}m{v}_{0}^{2}$=μmgcos37°sBC+Ep;
代入数据解得 Ep=19.4J
(2)小物块在沿轨道运动的过程中,系统产生的热量 Q=μmgcos37°sBC=4J
(3)设物块由弹簧反弹上升到与O等高的点时初速度为v.
则对整个过程,由能量守恒定律得:
$\frac{1}{2}m{v}^{2}$=2μmgcos37°sBC+mgRsin53°
解得 v=4m/s
所以使小物块在沿轨道运动的过程中不脱离轨道,vB的范围为 vB≤4m/s
答:
(1)弹簧被压缩到D点时的弹性势能Ep是19.4J.
(2)小物块在沿轨道运动的过程中,系统产生的热量Q是4J.
(3)使小物块在沿轨道运动的过程中不脱离轨道,vB的范围为 vB≤4m/s.
点评 该题的关键理清物体的运动情况,搞清能量是怎样转化,分段运用能量守恒定律进行列式.要知道隐含的临界状态:物块恰好到达与圆心等高的点,速度为零.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
14.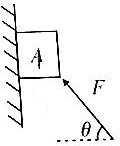 如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
 如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )| A. | 物体A受到4个力作用 | B. | mg=Fcosθ | ||
| C. | 物体A对墙的压力为Fcosθ | D. | 撤去F后,物体A做自由落体运动 |
19.物理学史上有很多物理学家做出具大的贡献,以下叙述正确的是( )
| A. | 牛顿发现了万有引力定律并测出了引力常量 | |
| B. | 伽利略通过对物体运动的研究,提出了“力是维持物体运动的原因”这一观点 | |
| C. | 法拉第首先发现了电磁感应现象,使人们能够成功地将机械能转化为电能 | |
| D. | 安培发现了电流能产生磁场,并提出了著名的分子电流假说 |
16.请认真分析下列图中的情景:图a中,物体A、B、C叠放在水平桌面上,水平力F作用于C物体上,使A、B、C以共同速度向右匀速运动;图b中,另一端与斜面体P连接,P与固定挡板MN接触且P处于静止状态;图c中,小车M在恒力F作用下,沿水平地面(光滑、粗糙,情况未知)做直线运动,下列选项正确的是( )


| A. | 图a中A受5个力作用,B受2个力作用,C受4个力作用 | |
| B. | 图b中P受到的外力个数可能为2个或者4个 | |
| C. | 图c中若小车做做匀速运动,则小车一定受4个力作用 | |
| D. | 图c中若小车做加速运动,则小车可能受3个力作用 |
20. 有一条捕鱼小船停靠在湖边码头,小船又窄又长,甲同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行码头自由停泊,然后他轻轻从船尾上船,走到船头后停下,另外一位同学用卷尺测出船后退的距离d,然后用卷尺测出船长L.已知甲同学的质量为m,则渔船的质量为( )
有一条捕鱼小船停靠在湖边码头,小船又窄又长,甲同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行码头自由停泊,然后他轻轻从船尾上船,走到船头后停下,另外一位同学用卷尺测出船后退的距离d,然后用卷尺测出船长L.已知甲同学的质量为m,则渔船的质量为( )
 有一条捕鱼小船停靠在湖边码头,小船又窄又长,甲同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行码头自由停泊,然后他轻轻从船尾上船,走到船头后停下,另外一位同学用卷尺测出船后退的距离d,然后用卷尺测出船长L.已知甲同学的质量为m,则渔船的质量为( )
有一条捕鱼小船停靠在湖边码头,小船又窄又长,甲同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行码头自由停泊,然后他轻轻从船尾上船,走到船头后停下,另外一位同学用卷尺测出船后退的距离d,然后用卷尺测出船长L.已知甲同学的质量为m,则渔船的质量为( )| A. | $\frac{m(L+d)}{d}$ | B. | $\frac{m(L-d)}{d}$ | C. | $\frac{mL}{d}$ | D. | $\frac{m(L+d)}{L}$ |
17.有关光的现象,下列说法正确的是( )
| A. | 光从水中到空气中折射时,频率不变而波长变长 | |
| B. | 光在光导纤维中传播时,在纤维与空气的界面上发生全反射 | |
| C. | 观看立体电影的眼镜利用光的干涉原理制成 | |
| D. | 紫外线具有显著的荧光效应,波长比可见光更长 |
 如图所示,有一质量为m=1.0kg的滑块从光滑曲面轨道顶点A由静止滑至粗糙的水平面的C点而停止.曲面轨道顶点离地面高度为H=0.8m.已知
如图所示,有一质量为m=1.0kg的滑块从光滑曲面轨道顶点A由静止滑至粗糙的水平面的C点而停止.曲面轨道顶点离地面高度为H=0.8m.已知 某同学为了探究质量均匀分布的直杆转动时的转动惯量,设计了如图所示的实验:
某同学为了探究质量均匀分布的直杆转动时的转动惯量,设计了如图所示的实验: 如图所示,匀强磁场的磁感应强度B=$\frac{1}{2}$T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=2Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度为ω=10$\sqrt{2}$rad/s,外电路电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=$\frac{1}{2}$T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=2Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度为ω=10$\sqrt{2}$rad/s,外电路电阻R=4Ω,求: