题目内容
10.质量m=4kg的物体,与水平地面间的动摩擦因数μ=0.1,沿水平地面向右做直线运动,经过A点时速度为6m/s,物体经过A点时开始计时并对物体施加水平向左的恒力F=12N,g取10m/s2.(1)若1.5s末撒去F,物体停在B点,求B与A的距离;
(2)若t时刻撤去F,物体最后停在A点右方3.75m处的C点,求F的作用时间t.
分析 (1)根据牛顿第二定律求解加速度大小,再根据速度时间关系求解物体减速运动时间,最后求解位移大小;
(2)根据动能定理求解拉力F从B点开始反向运动的位移,根据牛顿第二定律求解加速度,再根据位移时间关系求解时间.
解答 解:(1)对物体施加水平向左的恒力F=12N时加速度为a,根据牛顿第二定律可得:
$a=\frac{F+μmg}{m}=\frac{12+0.1×40}{4}m/{s}^{2}=4m/{s}^{2}$,
物体减速到零经过的时间为:${t}_{1}=\frac{{v}_{A}}{a}=\frac{6}{4}s=1.5s$,
所以去掉力F时物体速度刚好为零,则位移为:
${x}_{1}=\frac{{v}_{A}+0}{2}{t}_{1}=\frac{6}{2}×1.5m=4.5m$;
(2)根据(1)可知,在1.5s时物体速度为零,位移为4.5m,如果此时拉力没有撤去,物体会反向运动;
反向运动的距离为L=4.5m-3.75m=0.75m,
设反向运动位移为x时拉力撤去,根据动能定理可得:
Fx-μmgL=0,
解得:$x=\frac{μmgL}{F}=\frac{0.1×40×0.75}{12}m=0.25m$,
此过程的加速度大小为:$a′=\frac{F-μmg}{m}=\frac{12-0.1×40}{4}m/{s}^{2}=2m/{s}^{2}$,
根据位移时间关系可得:x=$\frac{1}{2}a{{t}_{2}}^{2}$,
解得:t2=0.5s;
所以力F的作用时间为:t=t1+t2=1.5s+0.5s=2s.
答:(1)若1.5s末撒去F,物体停在B点,则B与A的距离为4.5m;
(2)若t时刻撤去F,物体最后停在A点右方3.75m处的C点,则F的作用时间为2s.
点评 对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.

 阅读快车系列答案
阅读快车系列答案 如图所示,A物块质量为2m,B物块质量为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触,此时弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,以下说法正确的是( )
如图所示,A物块质量为2m,B物块质量为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触,此时弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,以下说法正确的是( )| A. | 悬绳剪断瞬间,A物块的加速度大小为$\frac{3}{2}$g | |
| B. | 悬绳剪断瞬间,A物块的加速度大小为2g | |
| C. | 悬绳剪断瞬间,A物块向下运动距离x时速度最大 | |
| D. | 悬绳剪断瞬间,A物块向下运动距离3x时速度最大 |
 如图所示,两根长度均为L的刚性轻杆,一端通过质量为m的球形铰链a连接,另一端分别与两个质量均为m小球b、c相连.将此装置的两杆合拢,铰链a在上、竖直地放在水平桌面上,然后轻敲一下,使两小球向两边对称滑动,但两杆始终保持在竖直平面内.忽略一切摩擦,则下列说法正确的是( )
如图所示,两根长度均为L的刚性轻杆,一端通过质量为m的球形铰链a连接,另一端分别与两个质量均为m小球b、c相连.将此装置的两杆合拢,铰链a在上、竖直地放在水平桌面上,然后轻敲一下,使两小球向两边对称滑动,但两杆始终保持在竖直平面内.忽略一切摩擦,则下列说法正确的是( )| A. | a落地前,轻杆对b、c一直做正功 | |
| B. | a下落过程中,其加速度大小始终小于g | |
| C. | a落地时速度大小为$\sqrt{2gL}$ | |
| D. | a落地前,当a的机械能最小时,b、c对地面的压力大小为mg |
 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于电容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离,则( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于电容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离,则( )| A. | 带电油滴将沿竖直方向向上运动 | B. | P点的电势将降低 | ||
| C. | 带电油滴的电势能将减少 | D. | 极板带电荷量将减少 |
| A. | 开普勒进行了“月-地检验”,得出天上和地下的物体都遵从万有引力定律的结论 | |
| B. | 哥白尼提出“日心说”,发现了太阳系中行星沿椭圆轨道运动的规律 | |
| C. | 第谷通过对天体运动的长期观察,发现了行星运动三定律 | |
| D. | 牛顿发现了万有引力定律,卡文迪许测定出引力常量G |




 如图所示,两根足够长平行金属导轨MN、PQ固定在倾角θ=37°的绝缘斜面上,顶部接有一阻值R=3Ω的定值电阻,下端开口,轨道间距L=1m.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直斜面向上.质量m=1kg的金属棒ab置于导轨上,ab在导轨之间的电阻r=1Ω,电路中其余电阻不计.金属棒ab由静止释放后沿导轨运动时始终垂直于导轨且与导轨接触良好.已知金属棒ab与导轨间动摩擦因数μ=0.5,不计空气阻力影响.sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
如图所示,两根足够长平行金属导轨MN、PQ固定在倾角θ=37°的绝缘斜面上,顶部接有一阻值R=3Ω的定值电阻,下端开口,轨道间距L=1m.整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直斜面向上.质量m=1kg的金属棒ab置于导轨上,ab在导轨之间的电阻r=1Ω,电路中其余电阻不计.金属棒ab由静止释放后沿导轨运动时始终垂直于导轨且与导轨接触良好.已知金属棒ab与导轨间动摩擦因数μ=0.5,不计空气阻力影响.sin37°=0.6,cos37°=0.8,取g=10m/s2.求: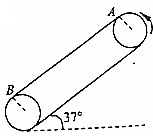 某工厂流水线车间传送带如图所示:逆时针匀速转动的传送带长L=4m,与水平面夹角为37°;小工件被一个接一个地静止放到传送带顶端A点,小工件与传送带间的动摩擦因数μ=0.25;则在这些小工件被运送到底端B点过程中,求:
某工厂流水线车间传送带如图所示:逆时针匀速转动的传送带长L=4m,与水平面夹角为37°;小工件被一个接一个地静止放到传送带顶端A点,小工件与传送带间的动摩擦因数μ=0.25;则在这些小工件被运送到底端B点过程中,求: