��Ŀ����
3�����Ϻ���Ϣ������3���ҹ������ˡ�̽�¼ƻ�����Ԥ����3�����̽�����ǣ���̽�¼ƻ�����Ҫ�����һ���ؼ������ǣ��������̽�����ǽ�������������Ϊ�ˣ��Ϻ����������ˡ���ȡ�༶�ƽ��ķ�ʽ��̽�����������������ķ����������˷����������ȱ�����һ������ͬ����Բ���A����һ���A������������Ϊ500�����ԶΪ7���̽�����ǽ���26Сʱ���ƴ˹��һȦ��Ȼ��ͨ����ȡ�����������ٽ���һ���������Բ���B�����������������Ϊ500�����ԶΪ12����˺�̽�����Dz��ϻ�����������ֱ�ӡ��������쵽����ʱ���������ƻ���ķ������Ƽ��٣�����������Ȧ��������Ϊ���������ǣ������������200����߶ȵ����ع��C�Ϸ��У�Ϊ����������½��������֪��������m���������M�ı�ֵΪ$\frac{m}{M}=\frac{1}{81}$������뾶r�����뾶R֮��Ϊ$\frac{r}{R}$=0.273������뾶RΪ6371km���Ը�����������������ж������⣺
��1��̽�������ڵ���ͬ����Բ���A��B�Ϸ���ʱ������֮�ȣ���ȡһλ��Ч���֣�
��2��̽�������ڻ�������C�Ϸ��е����ڣ�
���� ��1�����ݿ����յ������ɼ���������A��B�Ϸ���ʱ������֮�ȣ�
��2�������������ṩ�����������ڹ�ʽ�����Եõ����ڵ���ֵ��
��� �⣺��1�����ݿ����յ������ɣ�$\frac{{R}_{A}^{3}}{{T}_{A}^{2}}=\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$
���ԣ�$\frac{{T}_{A}}{{T}_{B}}=\sqrt{��\frac{{R}_{A}}{{R}_{B}}��^{3}}$=$\sqrt{��\frac{\frac{6371+500+6371+70000}{2}}{\frac{6371+500+6371+120000}{2}}��^{3}}$��0.5
��2�����Ƕ����ǣ������������ṩ����������A�����
$\frac{GM{m}_{0}}{{R}_{A}^{2}}={m}_{0}•��\frac{2��}{{T}_{A}}��^{2}•{R}_{A}$����
������C������˶�ʱ��
$\frac{Gm{m}_{0}}{{r}^{2}}={m}_{0}•{��\frac{2��}{{T}_{C}}��}^{2}•r$����
�����٢ڵã�$\frac{{T}_{C}^{2}}{{T}_{A}^{2}}=\frac{M}{m}•\frac{{r}^{3}}{{R}_{A}^{3}}$
�֣�r=0.273R=0.273��6731=1838km
${R}_{A}=\frac{6371+500+6371+70000}{2}=41621$km
�������ݵã�TC=2.17h=7815s
�𣺣�1��̽�������ڵ���ͬ����Բ���A��B�Ϸ���ʱ������֮����0.5��
��2��̽�������ڻ�������C�Ϸ��е�������7815s��
���� �����������ͣ��ؼ���������������Դ�����������������ɡ�ţ�ٵڶ����ɺ�Բ���˶��Ĺ�����ʽ���з������ɣ�

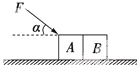 ��ͼ��ʾ������A��B�����䶯Ħ��������ͬ������Ҳ��ͬ������F��������һ����ˮƽ�����˶��˾���s������˵������ȷ���ǣ�������
��ͼ��ʾ������A��B�����䶯Ħ��������ͬ������Ҳ��ͬ������F��������һ����ˮƽ�����˶��˾���s������˵������ȷ���ǣ�������| A�� | Ħ������A��B�����Ĺ���ͬ | B�� | ��������A��B�����Ĺ���ͬ | ||
| C�� | F��A�����Ĺ���A��B���Ĺ���ͬ | D�� | A��B������������B��A�������� |
| A�� | 16.2�� | B�� | 32.4�� | C�� | 360K | D�� | 180K |
| A�� | ���ؾ������������������ | |
| B�� | ��ȫʧ�ؾ��������������ʧ�� | |
| C�� | ��ֱ�����˶������岻�����ʧ������ | |
| D�� | ��ֱ�����˶���������ܻ���ֳ������� |
 ���в��ֹ�������װ�����ܻ��綯���ݣ���ͼ��ʾ�����˿�վ�Ϸ���ʱ�����Ȼ������٣�Ȼ��������������������
���в��ֹ�������װ�����ܻ��綯���ݣ���ͼ��ʾ�����˿�վ�Ϸ���ʱ�����Ȼ������٣�Ȼ��������������������| A�� | �˿�ʼ�մ��ڳ���״̬ | |
| B�� | �˿�ʼ�մ���ʧ��״̬ | |
| C�� | ���ݶԳ˿͵�������ʼ����ֱ���� | |
| D�� | ������������ʱ�����ݶԳ˿͵���������ֱ���� |
| A�� | �ڸ������������v0=$\frac{v}{x}$$\sqrt{2Rh}$�ij��ٶ�ˮƽ�׳�һ���壬���彫�������������� | |
| B�� | �ڸ������������v0=$\frac{v}{x}$$\sqrt{2Rh}$�ij��ٶ�ˮƽ�׳�һ���壬���彫���������� | |
| C�� | �ƾ������������ΪR���е����ǵ����ļ��ٶ�Ϊa=$\frac{2h{v}^{2}}{{x}^{2}}$ | |
| D�� | �Ƹ�������渽�����е����ǵ�����ΪT=$\frac{2��r}{v}$ |
| A�� | a1��a2=4��1 | B�� | ��1����2=2��1 | C�� | T1��T2=1��8 | D�� | r1��r2=1��2 |
 ��ͼ��ʾ����һ���Ϊ30���б���ϣ�һ��������A���ɾ�ֹ������ʼ���£���ǣ��������������£��н�45m����B�㣬��ʱ�رշ���������������ǰ��15m����C��ʱ�ٶ�Ϊ�㣬��֪������̥�����䶯Ħ������Ϊ��=$\frac{\sqrt{3}}{6}$����������m=104kg��ȡg=10m/s2����
��ͼ��ʾ����һ���Ϊ30���б���ϣ�һ��������A���ɾ�ֹ������ʼ���£���ǣ��������������£��н�45m����B�㣬��ʱ�رշ���������������ǰ��15m����C��ʱ�ٶ�Ϊ�㣬��֪������̥�����䶯Ħ������Ϊ��=$\frac{\sqrt{3}}{6}$����������m=104kg��ȡg=10m/s2����