题目内容
8.用手托一小球,竖直向上抛出,再接住小球,将这一过程简化为下面的理想运动模型:手托小球由静止开始,先竖直向上做匀加速运动,然后再做匀减速运动,手停下后在该处接住落回的小球使小球做匀减速运动.已知匀加速运动的加速度为4m/s2,加速运动距离为0.5m,匀减速运动加速度大小为20m/s2,重力加速度取10m/s2,求小球运动的最大速度和总时间.分析 当小球离开手时的速度最大,结合速度位移公式求出小球的最大速度.根据速度时间公式分别求出匀加速、竖直上抛和匀减速运动的时间,从而得出总时间.
解答 解:当小球离开手时,速度最大,根据速度位移公式得:
v2=2ax1,
解得:$v=\sqrt{2a{x}_{1}}=\sqrt{2×4×0.5}$m/s=2m/s.
小球匀加速直线运动的时间为:${t}_{1}=\frac{v}{a}=\frac{2}{4}s=0.5s$,
小球竖直上抛上升的时间${t}_{2}=\frac{v}{g}=\frac{2}{10}s=0.2s$,竖直上抛上升的位移${x}_{2}=\frac{{v}^{2}}{2g}=\frac{4}{20}m=0.2m$,
手向上匀减速直线运动的位移${x}_{3}=\frac{{v}^{2}}{2{a}_{2}}=\frac{4}{40}m=0.1m$,
则小球竖直上抛时下降的位移大小x4=x2-x3=0.2-0.1m=0.1m,
下降的时间${t}_{3}=\sqrt{\frac{2{x}_{4}}{g}}=\sqrt{\frac{2×0.1}{10}}s≈0.14s$,
小球返回手中的速度v′=gt3=10×0.14m/s=1.4m/s,
向下匀减速运动的时间${t}_{4}=\frac{v′}{{a}_{2}}=\frac{1.4}{20}s=0.07s$,
则总时间t=t=t1+t2+t3+t4=0.5+0.2+0.14+0.07s=0.91s.
答:小球运动的最大速度为2m/s,总时间为0.91s.
点评 解决本题的关键理清小球在整个过程中的运动规律,结合运动学公式灵活求解,难度不大.

练习册系列答案
相关题目
18.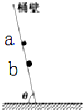 “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示为剖面图,已知桶壁的倾角为θ,两个演员的车和人的总质量为ma、mb,且ma>mb.若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示为剖面图,已知桶壁的倾角为θ,两个演员的车和人的总质量为ma、mb,且ma>mb.若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
 “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示为剖面图,已知桶壁的倾角为θ,两个演员的车和人的总质量为ma、mb,且ma>mb.若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示为剖面图,已知桶壁的倾角为θ,两个演员的车和人的总质量为ma、mb,且ma>mb.若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )| A. | 二者的速度相同 | B. | a处于高处,a的速度更大一些 | ||
| C. | 桶面对a和b支持力是一样的 | D. | a和b的加速度大小是一样的 |
19.下列电磁波中,波长最短的是( )
| A. | 无线电波 | B. | 红外线 | C. | γ射线 | D. | 紫外线 |
3.A、B为两等量异种电荷,图中水平虚线为A、B连线的中垂线,现将另两个等量异种的检验电荷a、b,如图用绝缘细杆连接后从离AB无穷远处沿中垂线平移到AB的连线,平移过程中两检验电荷位置始终关于中垂线对称.若规定离AB无穷远处电势为零,则下列说法中正确的是( )


| A. | 在AB的连线上a所处的位置电势φa<0 | |
| B. | a、b整体在AB连线处具有的电势能Ep>0 | |
| C. | 整个移动过程中,静电力对a做正功 | |
| D. | 整个移动过程中,静电力对a、b整体做正功 |
20. 如图所示,一半径为R=0.5m,粗糙程度均匀的半圆形轨道竖直固定在水平面上,直径MN水平,一可视为质点的小球自M点由静止开始下落,由于摩擦阻力的作用,来回滑动数次后最终停在轨道底部,若小球到达右侧的最高位置为P点,P距地面的高度h1=0.4m,小球到达左侧除M点外最高位置为Q点,则关于Q距地面的高度h2的值可能正确的是( )
如图所示,一半径为R=0.5m,粗糙程度均匀的半圆形轨道竖直固定在水平面上,直径MN水平,一可视为质点的小球自M点由静止开始下落,由于摩擦阻力的作用,来回滑动数次后最终停在轨道底部,若小球到达右侧的最高位置为P点,P距地面的高度h1=0.4m,小球到达左侧除M点外最高位置为Q点,则关于Q距地面的高度h2的值可能正确的是( )
 如图所示,一半径为R=0.5m,粗糙程度均匀的半圆形轨道竖直固定在水平面上,直径MN水平,一可视为质点的小球自M点由静止开始下落,由于摩擦阻力的作用,来回滑动数次后最终停在轨道底部,若小球到达右侧的最高位置为P点,P距地面的高度h1=0.4m,小球到达左侧除M点外最高位置为Q点,则关于Q距地面的高度h2的值可能正确的是( )
如图所示,一半径为R=0.5m,粗糙程度均匀的半圆形轨道竖直固定在水平面上,直径MN水平,一可视为质点的小球自M点由静止开始下落,由于摩擦阻力的作用,来回滑动数次后最终停在轨道底部,若小球到达右侧的最高位置为P点,P距地面的高度h1=0.4m,小球到达左侧除M点外最高位置为Q点,则关于Q距地面的高度h2的值可能正确的是( )| A. | 0.32m | B. | 0.30m | C. | 0.28m | D. | 0.20m |
13.一个小球在液体里运动,会受到一种类似于摩擦的液体阻力的作用,叫做粘滞力.如果液体无限深广,计算粘滞力的关系式为F=3πDηv,其中D为小球直径,v为小球在液体中的运动速度,η称作粘滞系数.
实验创新小组的同学们通过下面实验测量了某液体的粘滞系数.

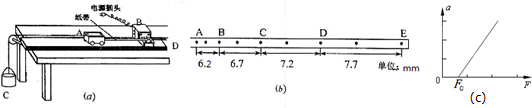
(1)取一个装满液体的大玻璃缸,放在水平桌面上,将质量为1kg的小钢球沉入液体底部,可以忽略除粘滞力以外的所有摩擦阻力的作用.将一根细线拴在小钢球上,细线另一端跨过定滑轮连接砝码盘.在玻璃缸内靠左端固定两个光电门A、B,光电门的感光点与小钢球的球心在同一条水平线上.
(2)测出小钢球直径为5.00cm,将钢球由玻璃缸底部右侧释放,调整砝码数量以及释放小钢球的初始位置,确保小钢球通过两个光电门的时间相同.若某次测出小钢球通过两个光电门的时间均为0.025s,则可得小钢球此时运动的速度大小为2.0m/s.
(3)记录此时砝码盘以及砝码的总质量m=60g,由计算粘滞力的关系式可得液体的粘滞系数为η=0.62N•s/m2.
(4)改变砝码数量,重复第(2)、(3)步骤的实验,测出不同质量的砝码作用下,小钢球匀速运动速度.由表中数据,描点连线,作出粘滞力随速度变化的图象(如图2).
根据计算粘滞力的关系式和图象,可得该液体的粘滞系数为η=0.48N•s/m2.(所有结果均保留两位有效数字)
实验创新小组的同学们通过下面实验测量了某液体的粘滞系数.

(1)取一个装满液体的大玻璃缸,放在水平桌面上,将质量为1kg的小钢球沉入液体底部,可以忽略除粘滞力以外的所有摩擦阻力的作用.将一根细线拴在小钢球上,细线另一端跨过定滑轮连接砝码盘.在玻璃缸内靠左端固定两个光电门A、B,光电门的感光点与小钢球的球心在同一条水平线上.
(2)测出小钢球直径为5.00cm,将钢球由玻璃缸底部右侧释放,调整砝码数量以及释放小钢球的初始位置,确保小钢球通过两个光电门的时间相同.若某次测出小钢球通过两个光电门的时间均为0.025s,则可得小钢球此时运动的速度大小为2.0m/s.
(3)记录此时砝码盘以及砝码的总质量m=60g,由计算粘滞力的关系式可得液体的粘滞系数为η=0.62N•s/m2.
(4)改变砝码数量,重复第(2)、(3)步骤的实验,测出不同质量的砝码作用下,小钢球匀速运动速度.由表中数据,描点连线,作出粘滞力随速度变化的图象(如图2).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 砝码盘以及砝码的总质量m/g | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 粘滞力F/N | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 1.0 |
| 小钢球匀速运动速度v/m•s-1 | 1.3 | 1.8 | 2.2 | 2.0 | 3.1 | 3.5 | 4.0 | 4.4 |
 如图所示为某学生为游乐园设计的一个表演装置,设计的目的是利用左边的圆周运动装置将一只装在保护球里的表演猴子水球一起抛上表演台,工作时将保护球安装在转动杆的末端,转动杆的长度L=2.5cm,杆被安装在支架上的电动机带动而匀速转动.已知猴子和保护球的总质量m=5kg;当杆转动到竖直方向成60°角时,保护球与杆脱离连接并被抛出,保护球到达水平表演台时,速度方向水平,大小v2=2.5m/s,忽略空气阻力,g取10m/s2,求:
如图所示为某学生为游乐园设计的一个表演装置,设计的目的是利用左边的圆周运动装置将一只装在保护球里的表演猴子水球一起抛上表演台,工作时将保护球安装在转动杆的末端,转动杆的长度L=2.5cm,杆被安装在支架上的电动机带动而匀速转动.已知猴子和保护球的总质量m=5kg;当杆转动到竖直方向成60°角时,保护球与杆脱离连接并被抛出,保护球到达水平表演台时,速度方向水平,大小v2=2.5m/s,忽略空气阻力,g取10m/s2,求: