题目内容
13．
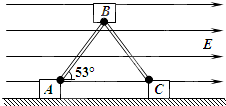如图所示，两个长均为L的轻质杆，通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连，整体处于竖直面内．A、C为两个完全相同的小物块，B物块的质量与A小物块的质量之比为2：1，三个物块的大小都可忽略不计．A、C两物块分别带有+q、-q的电荷量，并置于绝缘水平面上，在水平面上方有水平向右的匀强电场，场强为E，物块间的库仑力不计．当AB、BC与水平面间的夹角均为53°时，整体恰好处于静止状态，一切摩擦均不计，并且在运动过程中无内能产生，重力加速度为g，（sin53°=0.8，cos53°=0.6），则B物块的质量为$\frac{8Eq}{3g}$；若将B物块略向下移动一些，并由静止释放，则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$．
分析 当AB、BC与水平面间的夹角均为53°时，整体恰好处于静止状态，分别以A、B为研究对象，根据平衡条件求出物块B的质量．
B物块向下运动的过程中，重力和电场力做功．B物块落地前的瞬间A、C的速度恰好为零，根据动能定理求出B物块到达地面前瞬时速度的大小．
解答 解：以A为研究对象，如图1所，F为轻质杆的弹力大小，
则由平衡条件得
Fcos53°=Eq
得：F=$\frac{5}{3}$Eq
以B为研究对象，如图2，Mg为B物块的重力，则有 2Fsin53°=Mg
得：M=$\frac{8Eq}{3g}$
（2）B物块向下做加速度增大的加速运动，一直到B物块落地．以整体为研究对象，有重力和电场力做功，设B物块落地前的瞬间速度大小为v，此时A、C的速度恰好为零，根据动能定理得
MgLsin53°-2Eq（L-Lcos53°）=$\frac{1}{2}$Mv2；
解得，v=$\sqrt{gL}$
故答案为：$\frac{8Eq}{3g}$，$\sqrt{gL}$．
点评 本题第1问是三个物体的平衡问题，采用隔离法研究是常用的思路．第2问难点是确定B物块落地前的瞬间A、C的速度均为零，可利用装置的对称性理解．
练习册系列答案
相关题目
3．
在竖直向上的拉力F作用下，将货物由地面吊起，其运动的v2-x图象如图所示（取g=10m/s2）．则前3m内与最后2m内拉力的大小之比（ ）
在竖直向上的拉力F作用下，将货物由地面吊起，其运动的v2-x图象如图所示（取g=10m/s2）．则前3m内与最后2m内拉力的大小之比（ ）| A． | 12：7 | B． | 22：17 | C． | 22：23 | D． | 18：23 |
如图所示，R1=10Ω，R2=4Ω，R3=6Ω，R4=3Ω，AB间所加电压U=2.4V．若在C、D之间接一个伏特表，它的读数是1.8V；若在C、D之间接一个安培表，则它的读数是0.67A．
在测电源电动势和内电阻的实验中得到的实验图线如图所示，图中U为路端电压，I为干路电流，a、b为图线上的两点，相应状态下电源的效率分别为ηa、ηb．由图可知ηa=66.7%，ηb=33.3%．
8．
如图所示，一列简谐波向右以8.0m/s的速度传播，某一时刻沿波的传播方向上有a、b两质点，位移大小相等，方向相同，则（ ）
如图所示，一列简谐波向右以8.0m/s的速度传播，某一时刻沿波的传播方向上有a、b两质点，位移大小相等，方向相同，则（ ）| A． | 无论再经多长时间，a、b两质点位移不可能大小相等、方向相反 | |
| B． | 再经过0.25s，a、b两质点位移第一次大小相等、方向相反 | |
| C． | 再经过0.25s，a、b两质点速度第一次大小相等、方向相反 | |
| D． | 再经过0.5s，a、b两质点速度第一次大小相等、方向相同 |
一列横波沿x轴传播，t1时刻的波形如图中实线所示，t2时刻的波形如图中虚线所示．已知t2=（t1+1$\frac{3}{8}$）s，振源振动周期为0.5s，则波的传播方向是沿x轴正方向，从t1时刻到t2时刻波传播距离是16.5m．
4．一人造地球卫星绕地球做匀速圆周运动，假如该卫星变轨后仍做匀速圆周运动，速度减小为原来的$\frac{1}{2}$，不考虑卫星质量的变化，则变轨前后卫星的（ ）
| A． | 角速度之比为2：1 | B． | 向心加速度之比为4：1 | ||
| C． | 周期之比为1：8 | D． | 向心力之比为16：1 |
某同学设计了一个实验来感受向心力．如图甲所示，用一根细绳（可视为轻绳）一端拴一个小物体，绳上离小物体20cm处标为点A，40cm处标为点B．将此装置放在光滑水平桌面上（如图乙所示）抡动细绳，使小物体做匀速圆周运动，请另一位同学帮助用秒表计时．