题目内容
18.如图所示,质量为m=4t的汽车以恒定功率P=60kW从A点出发,先沿着长度为s1=400m,倾角为α的斜面(sinα=0.02)运动到B(其受到的阻力为车重k1=0.1倍),随后沿着长度为s2=500m的水平面运动到C(其受到的阻力为车重k2=0.1倍).若汽车在AB、BC段、BA段最后均可达到匀速行驶,g取10m/s2.求:
(1)汽车在AB段达到匀速行驶时的速度v1为多大?A到B耗时t1为多少?
(2)为了省油,汽车发动机在BC段至少需工作多久才能到达C点?
(3)若汽车仍以此恒定功率先沿CB的水平面运动,随后沿BA的斜面运动到A点,则与原路径相比,通过计算说明哪种更省时?
分析 (1)由功率的表达式P=FV及动能定理可分别求出汽车在斜坡匀速行驶的速度与时间;
(2)根据动能定理可求出汽车发动机在BD段至少还需工作的时间;
(3)由汽车克服阻力做功相同,根据动能定理可知,末速度越大的汽车工作时间越长,从而由末速度来确定谁能更省时.
解答 解:(1)在AB段汽车匀速v1,$\frac{P}{v_1}={k_1}$mg+mgsinα,
得 v1=$\frac{P}{{{k_1}mg+mgsinα}}$=12.5m/s
耗时t1,由Pt1-k1mgs1-mgs1sinα=$\frac{1}{2}m{v}_{1}$2,
解得t1=417s
(2)汽车在AB段速度已达到匀速,若以v1为初速滑行汽车不能达到C点.设汽车发动机在BC段至少需工作t时间,才能使得汽车恰好能到达C点.
根据动能定理:Pt-k2mgs2=0-$\frac{1}{2}$mv12,
解得t=28.5s
(3)两个路径中汽车克服阻力做功相同.根据动能定理有:
Pt1′-W阻-mgs1sinα=$\frac{1}{2}$mv22,Pt2′-W阻+mgs1sinα=$\frac{1}{2}$mv32,
在BC段汽车达到匀速时,有:v2=$\frac{P}{{{k_2}mg}}$=15m/s,
从BA段下行达到匀速时,有:v3=$\frac{p}{{k}_{1}mg-mgsinα}=18.75$m/s
解得t1′=72.83s,t2′=66.39s,所以汽车沿原来路径耗时更多.
答:(1)汽车在AB段达到匀速行驶时的速度v1为12.5m/s,A到B耗时t1为417s;
(2)为了省油,汽车发动机在BC段至少需工作28.5s才能到达C点;
(3)汽车沿原来路径耗时更多.
点评 本题考查动能定理,并体现动能定理的过程重要性.同时要注意定理中的速度与位移是同一参考系,及功的正负.还要关注的是牵引力做功W=Pt.

| A. | 电梯的加速度大小为2m/s2 | |
| B. | 电梯的加速度方向竖直向下 | |
| C. | 电梯一定在竖直向下运动 | |
| D. | 小明对体重计的压力小于体重计对他的支持力 |
| A. | 同一列声波在各种介质中的波长是相同的 | |
| B. | 声波的频率越高,它在空气中传播的速度越快 | |
| C. | 人能辨别不同乐器同时发出的声音,证明声波不会发生干涉 | |
| D. | 声波可以绕过障碍物传播,即它可以发生衍射 |
 如图所示,粗细均匀的U形管,左管封闭一段空气柱,两侧水银面高度差为h,U形管两管间宽度为d,且d<h.现将U形管以O点为轴顺时针旋转90°,至两平行管水平,并保持U形管在竖直面内.设温度不变,管的直径可忽略不计,水银没有溢出,则( )
如图所示,粗细均匀的U形管,左管封闭一段空气柱,两侧水银面高度差为h,U形管两管间宽度为d,且d<h.现将U形管以O点为轴顺时针旋转90°,至两平行管水平,并保持U形管在竖直面内.设温度不变,管的直径可忽略不计,水银没有溢出,则( )| A. | 封闭端水银柱的长度h1增大,开口端水银柱的长度h2减小,静止时h1>h2,封闭气体压强增大 | |
| B. | 封闭端水银柱的长度h1减小,开口端水银柱的长度h2增大,静止时h1=h2,封闭气体压强不变 | |
| C. | 封闭端水银柱的长度h1减小,开口端水银柱的长度h2增大,静止时h1>h2,封闭气体压强增大 | |
| D. | 封闭端水银柱的长度h1减小,开口端水银柱的长度h2增大,静止时h1<h2,封闭气体压强减小 |
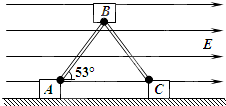 如图所示,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内.A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2:1,三个物块的大小都可忽略不计.A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计.当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g,(sin53°=0.8,cos53°=0.6),则B物块的质量为$\frac{8Eq}{3g}$;若将B物块略向下移动一些,并由静止释放,则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$.
如图所示,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内.A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2:1,三个物块的大小都可忽略不计.A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计.当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g,(sin53°=0.8,cos53°=0.6),则B物块的质量为$\frac{8Eq}{3g}$;若将B物块略向下移动一些,并由静止释放,则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$.



 如图所示,在水平向右的均强电场中固定一个斜面体,斜面体的高为H,斜面光滑且倾角为α,一质量为m的物块从斜面的底端以初速度v0沿斜面向上滑动,物块带电量为+q,电场强度大小E=$\frac{mgtanα}{q}$,求:
如图所示,在水平向右的均强电场中固定一个斜面体,斜面体的高为H,斜面光滑且倾角为α,一质量为m的物块从斜面的底端以初速度v0沿斜面向上滑动,物块带电量为+q,电场强度大小E=$\frac{mgtanα}{q}$,求: 一个轻质弹簧的劲度系数为k,一端固定,另一端在力的作用下发生的形变量为x,已知克服弹力所做的功等于弹簧弹性势能的增加量.(以上过程均在弹簧的弹性限度内)
一个轻质弹簧的劲度系数为k,一端固定,另一端在力的作用下发生的形变量为x,已知克服弹力所做的功等于弹簧弹性势能的增加量.(以上过程均在弹簧的弹性限度内) 如图所示,在水平地面上向右做匀速直线运动的汽车,通过定滑轮用绳子吊起一物体,若汽车和被吊物体在同一时刻的速度为v1和v2.
如图所示,在水平地面上向右做匀速直线运动的汽车,通过定滑轮用绳子吊起一物体,若汽车和被吊物体在同一时刻的速度为v1和v2.