题目内容
9. 如图所示,竖直放置的气缸由两个粗细不同的圆柱形筒组成.气缸中有A、B两个用长为L的细绳连接的活塞,它们的截面积分别为SA=20cm2,SB=10cm2,活塞A的质量MA=1kg,外界大气压P0=1.0×105Pa.当气缸内气体的压强P=1.2×105Pa,温度T=600K时,两活塞处于静止,此时两活塞到气缸连接处的高度都为$\frac{L}{2}$,则活塞B的质量MB=1kg.当气缸内气体的温度降到270K时,活塞B距离两气缸连接处的高度为0.9L(活塞与缸壁间的摩擦不计,气体始终无泄漏).
如图所示,竖直放置的气缸由两个粗细不同的圆柱形筒组成.气缸中有A、B两个用长为L的细绳连接的活塞,它们的截面积分别为SA=20cm2,SB=10cm2,活塞A的质量MA=1kg,外界大气压P0=1.0×105Pa.当气缸内气体的压强P=1.2×105Pa,温度T=600K时,两活塞处于静止,此时两活塞到气缸连接处的高度都为$\frac{L}{2}$,则活塞B的质量MB=1kg.当气缸内气体的温度降到270K时,活塞B距离两气缸连接处的高度为0.9L(活塞与缸壁间的摩擦不计,气体始终无泄漏).
分析 对AB活塞整体进行受力分析,根据受力平衡求出B活塞的质量;温度降低后,AB活塞下移,根据等压变化的规律,求出下移的距离,即可求出B活塞距离两汽缸连接处的距离
解答 解:以A、B两活塞和轻绳组成的系统为研究对象,
${p}_{0}^{\;}{S}_{A}^{\;}+p{S}_{B}^{\;}+({m}_{A}^{\;}+{m}_{B}^{\;})g=p{S}_{A}^{\;}+{p}_{0}^{\;}{S}_{B}^{\;}$
代入数据解得:${m}_{B}^{\;}=1kg$
缸内气体温度下降,气体体积减小,活塞下移,设A活塞下移x,缸内气体发生等压变化,根据盖-吕萨克定律有
初态:${V}_{1}^{\;}=\frac{L}{2}({S}_{A}^{\;}+{S}_{B}^{\;})$ ${T}_{1}^{\;}=600K$
末态:${V}_{2}^{\;}={S}_{A}^{\;}(\frac{L}{2}-x)+{S}_{B}^{\;}(\frac{L}{2}+x)$ ${T}_{2}^{\;}=270K$
根据$\frac{{V}_{1}^{\;}}{{T}_{1}^{\;}}=\frac{{V}_{2}^{\;}}{{T}_{2}^{\;}}$
代入上式:$\frac{\frac{L}{2}({S}_{A}^{\;}+{S}_{B}^{\;})}{{T}_{1}^{\;}}=\frac{{S}_{A}^{\;}(\frac{L}{2}-x)+{S}_{B}^{\;}(\frac{L}{2}+x)}{{T}_{2}^{\;}}$
解得:x=0.4L
活塞B距离两汽缸连接处的距离为$\frac{L}{2}+0.4L=0.9L$
故答案为:1,0.9
点评 本题的解题关键是分析气缸中气体做何种变化,根据力学知识求B活塞的质量,根据气体的状态变化过程,选择相应的实验定律都是应具备的解题能力.

| A. | 当f<f0时,该振动系统的振幅随f增大而减小 | |
| B. | 当f>f0时,该振动系统的振幅随f减小而增大 | |
| C. | 该振动系统的振动稳定后,振动的频率等于f0 | |
| D. | 该振动系统的振动稳定后,振动的频率等于f0的整数倍 |
| A. | W=8.0×104J△u=1.2×105J Q=4×104J | |
| B. | W=8.0×104J△u=-1.2×105J Q=-2×105J | |
| C. | W=8.0×104J△u=1.2×105J Q=2×105J | |
| D. | W=-8.0×104J△u=1.2×105J Q=2×105J |
| A. | 具有的重力势能相等 | B. | 所具有的机械能相等 | ||
| C. | 重力做的功不相等 | D. | 所具有的动能相等 |
 一质点在一个半圆球顶点以水平速度v=$\sqrt{gR}$飞出,试证明,此小球从此时刻后不会与圆球面相碰,并求出它的落地点与圆心的距离.
一质点在一个半圆球顶点以水平速度v=$\sqrt{gR}$飞出,试证明,此小球从此时刻后不会与圆球面相碰,并求出它的落地点与圆心的距离. 如图所示,水平桌面上叠放着一质量为m=1kg的金属块A(可看作质点)和质量为M=2kg的木板B,B的长度L=3.5m,A和B之间、B与地面之间的动摩擦因数分别为μ1=0.4,μ2=0.1.现对A施加大小为5N、水平向右的恒力F,同时给B一个瞬时作用使B获得向左的初速度Vo,Vo=3.5m/s,则(g取10m/s2)
如图所示,水平桌面上叠放着一质量为m=1kg的金属块A(可看作质点)和质量为M=2kg的木板B,B的长度L=3.5m,A和B之间、B与地面之间的动摩擦因数分别为μ1=0.4,μ2=0.1.现对A施加大小为5N、水平向右的恒力F,同时给B一个瞬时作用使B获得向左的初速度Vo,Vo=3.5m/s,则(g取10m/s2)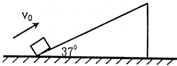 质量m=1kg物体,以v0=20m/s的初速度滑上一倾角为θ=37°的固定斜面,经2s到在最高点后又沿斜面滑下.以下两小题中距离和速度请用动能定理求解(g取10m/s2)
质量m=1kg物体,以v0=20m/s的初速度滑上一倾角为θ=37°的固定斜面,经2s到在最高点后又沿斜面滑下.以下两小题中距离和速度请用动能定理求解(g取10m/s2)