��Ŀ����
8��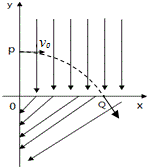 ��ͼ��ʾ���ڿռ佨��ƽ��ֱ������ϵ���ڵ�һ�����ڼ��ϵ糡ǿ�ȴ�СΪE��������-y�᷽�����ǿ�糡�����������ڼ��ϵ糡ǿ�ȴ�СҲΪE��������-x�᷽���ijһ�нǵ���ǿ�糡������һ����Ϊm���������+q�IJ�������������y����ij��P��ʼ�Գ��ٶ�v0��+x�᷽������һ���ޣ���ͨ������Ϊ��+x0��0����Q����Ժ͵��������ڵĵ糡��ֱ�ķ������������ޣ����ƿ�����������
��ͼ��ʾ���ڿռ佨��ƽ��ֱ������ϵ���ڵ�һ�����ڼ��ϵ糡ǿ�ȴ�СΪE��������-y�᷽�����ǿ�糡�����������ڼ��ϵ糡ǿ�ȴ�СҲΪE��������-x�᷽���ijһ�нǵ���ǿ�糡������һ����Ϊm���������+q�IJ�������������y����ij��P��ʼ�Գ��ٶ�v0��+x�᷽������һ���ޣ���ͨ������Ϊ��+x0��0����Q����Ժ͵��������ڵĵ糡��ֱ�ķ������������ޣ����ƿ�������������1��P������꣮
��2��������Q��ʱ���ٶȣ�
��3�����ӽ����������ʼ���˶���������������õ�ʱ�䣮
���� ��1�������ڵ�һ��������ƽ���˶������ţ�ٵڶ����ɺ��˶�ѧ��ʽ��ץס��ʱ�������ֱ�����ϵ�λ�ƣ��Ӷ��ó�P������꣮
��2�������ٶ�ʱ�乫ʽ�����ֱ���ٶȣ����ƽ���ı��ζ������Q����ٶȣ�
��3������ƽ���ı��ζ�����������������ʱ�ٶ���ˮƽ����ļнǣ������ڵ�������Ҳ������ƽ���˶������ٶȷ�����ֱ����ʱ�˶�������������ֵ�����ţ�ٵڶ����ɺ��ٶ�ʱ�乫ʽ����˶���ʱ�䣮
��� �⣺��1�������ڵ�һ����������ƽ���˶�����ˮƽ�����ϵ��˶�ʱ��Ϊ��${t}_{1}=\frac{{x}_{0}}{{v}_{0}}$��
��ֱ�����ϵļ��ٶ�${a}_{1}=\frac{qE}{m}$������ֱ�����ϵ�λ��Ϊ��y=$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}=\frac{1}{2}��\frac{qE}{m}��\frac{{{x}_{0}}^{2}}{{{v}_{0}}^{2}}$=$\frac{qE{{x}_{0}}^{2}}{2m{{v}_{0}}^{2}}$��
��P���������0��$\frac{qE{{x}_{0}}^{2}}{2m{{v}_{0}}^{2}}$��
��2��������Q��ʱ��ֱ�����ϵ��ٶ�Ϊ��${v}_{y}={a}_{1}{t}_{1}=\frac{qE{x}_{0}}{m{v}_{0}}$��
����ƽ���ı��ζ���֪������Q��ʱ���ٶ�Ϊ��${v}_{Q}=\sqrt{{{v}_{0}}^{2}+\frac{{q}^{2}{E}^{2}{{x}_{0}}^{2}}{{m}^{2}{{v}_{0}}^{2}}}$��
��3�����ڵ��������У����ٶȵķ�����ֱ����ʱ���˶������������ֵ��
������������ʱ�ٶȷ�����x��ļн�Ϊ�ȣ����У�tan$��=\frac{{v}_{y}}{{v}_{0}}=\frac{qE{x}_{0}}{m{{v}_{0}}^{2}}$��
���ڵ���������Ҳ������ƽ���˶����ٶȷ�����ֱ����ʱ���ص糡������ٶ�����ֱ����ļн�Ϊ�ȣ�
���ص糡������ٶ�Ϊv�䣬
$tan��=\frac{v}{v��}$��
��ã�$v��=\frac{v}{tan��}=\sqrt{{{v}_{0}}^{2}+\frac{{q}^{2}{E}^{2}{{x}_{0}}^{2}}{{m}^{2}{{v}_{0}}^{2}}}\frac{m{{v}_{0}}^{2}}{qE{x}_{0}}$��
�����ӽ����������ʼ���˶���������������õ�ʱ��Ϊ��
$t��=\frac{v��}{{a}_{1}}$=$\sqrt{{{v}_{0}}^{2}+\frac{{q}^{2}{E}^{2}{{x}_{0}}^{2}}{{m}^{2}{{v}_{0}}^{2}}}\frac{{m}^{2}{{v}_{0}}^{2}}{{q}^{2}{E}^{2}{x}_{0}}$��
�𣺣�1��P�������Ϊ��0��$\frac{qE{{x}_{0}}^{2}}{2m{{v}_{0}}^{2}}$����
��2��������Q��ʱ���ٶ�Ϊ$\sqrt{{{v}_{0}}^{2}+\frac{{q}^{2}{E}^{2}{{x}_{0}}^{2}}{{m}^{2}{{v}_{0}}^{2}}}$��
��3�����ӽ����������ʼ���˶���������������õ�ʱ��Ϊ$\sqrt{{{v}_{0}}^{2}+\frac{{q}^{2}{E}^{2}{{x}_{0}}^{2}}{{m}^{2}{{v}_{0}}^{2}}}\frac{{m}^{2}{{v}_{0}}^{2}}{{q}^{2}{E}^{2}{x}_{0}}$��
���� �������Ĺؼ����մ�����ƽ���˶��ķ�����֪�������ڴ�ֱ�糡������������ֱ���˶������ص糡���������ȼ���ֱ���˶������ţ�ٵڶ����ɺ��˶�ѧ��ʽ�ۺ���⣮

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� Ƶ�ʲ�ͬ��������ɫ��1��2����ͬ������Ǵ�ͬһ������һ����������·����ͼ��ʾ������˵����ȷ���ǣ�������
Ƶ�ʲ�ͬ��������ɫ��1��2����ͬ������Ǵ�ͬһ������һ����������·����ͼ��ʾ������˵����ȷ���ǣ�������| A�� | �ڲ����е�ɫ��1�Ĵ����ٶȴ��ڵ�ɫ��2�Ĵ����ٶ� | |
| B�� | ��ͬһ�����У���ɫ��1�Ķ��Ƶ�ѹС�ڵ�ɫ��2 | |
| C�� | ��ͬһװ����˫�����ʵ�飬��ɫ��1�����Ƽ��һ��С�ڵ�ɫ��2 | |
| D�� | ��ɫ��1�Ӳ�����������ȫ�����ٽ��С�ڵ�ɫ��2�Ӳ�����������ȫ�����ٽ�� |
| A�� | �뾶r1��r2 | B�� | ����ת�����ٶȦ�1����2 | ||
| C�� | ����ת�����ļ��ٶ�a1��a2 | D�� | ������E1��E2 |

��1��ʵ���е���������ﵽʵ��Ҫ��ʱ��������ĸ�����ť��λ����ͼ����ʾ��������Ķ�����4000����
��2��Ϊ�˼�С��������θı������ĵ���R��������ѹ����ʾ��U���õ���������ݣ�����ͼ������ֽ�ϻ���$\frac{1}{U}$��R�Ĺ�ϵͼ�ߣ�
| ʵ����� | 1 | 2 | 3 | 4 | 5 | 6 |
| R/�� | 0 | 1000.0 | 2000.0 | 3000.0 | 4000.0 | 5000.0 |
| U/V | 2.89 | 2.17 | 1.74 | 1.45 | 1.24 | 1.09 |
| 1/U��/V-1�� | 0.35 | 0.46 | 0.58 | 0.69 | 0.81 | 0.92 |
��4����С��ͬѧ������Դ����������Ҫԭ�������B
A�����ߵĵ��� B����ѹ����������� C����ѹ�������� D��������ľ�ȷ�ȣ�
| A�� | ���Զ�������ɽ���Ͽ� | |
| B�� | ͬ�������ڵ��������ڳ���״̬ | |
| C�� | ͬ�����ǹ��ƽ���������ƽ���غϣ�ͬ������ֻ�������ڳ���Ͽ�ijһ�㶨�߶��� | |
| D�� | Ϊ����ͨ�������ڹ������ײ��Ӧʹ���������ڲ�ͬ�Ĺ���� |
 һ�м�г�Შ��x����������ijʱ�̵IJ���ͼ��ͼ��ʾ���Ӹ�ʱ�̿�ʼ��ʱ��
һ�м�г�Შ��x����������ijʱ�̵IJ���ͼ��ͼ��ʾ���Ӹ�ʱ�̿�ʼ��ʱ�� ԭ�ӿ��Դ�ԭ�Ӽ����ײ�л���������Ӷ������ܼ�ԾǨ������ײ�У�������ʧ��������ȫ�ǵ�����ײ��
ԭ�ӿ��Դ�ԭ�Ӽ����ײ�л���������Ӷ������ܼ�ԾǨ������ײ�У�������ʧ��������ȫ�ǵ�����ײ�� ����M=2kg�ij�ľ��A����ȿɺ��ԣ�����L=4m����ˮƽ���Ͼ�ֹ�������ҵ�ˮƽ����F=11N��ʹ����ٵ�v0=1m/s����ʱ������m=1kg��ľ��B��ľ���С�ɺ��ԣ�������ڳ�ľ����Ҷˣ��Ӵ�ʱ��ʱ����ʱ��t1ľ�鵽��ľ������뿪ľ�壬��ʱ��F��ȥ���ӳ�ȥF���پ���ʱ��t2ľ�龲ֹ����֪ľ��������Ķ�Ħ������Ϊ��1=0.2��ľ����ľ���Ħ��������2=0.1�����Ħ�������ڻ���Ħ��������g=10m/s2������
����M=2kg�ij�ľ��A����ȿɺ��ԣ�����L=4m����ˮƽ���Ͼ�ֹ�������ҵ�ˮƽ����F=11N��ʹ����ٵ�v0=1m/s����ʱ������m=1kg��ľ��B��ľ���С�ɺ��ԣ�������ڳ�ľ����Ҷˣ��Ӵ�ʱ��ʱ����ʱ��t1ľ�鵽��ľ������뿪ľ�壬��ʱ��F��ȥ���ӳ�ȥF���پ���ʱ��t2ľ�龲ֹ����֪ľ��������Ķ�Ħ������Ϊ��1=0.2��ľ����ľ���Ħ��������2=0.1�����Ħ�������ڻ���Ħ��������g=10m/s2������ ��ͼ��ʾ����xOyƽ���ڣ�x���Ϸ�����y�����ϵ��㹻�����ǿ�糡���糡���±߽�Ϊy1=0.5m��ֱ�ߣ���y����y2=1.0m����һ����ԴS��x������һ���㹻����ӫ����������ԴS����ͼ180�㷶Χ�ڣ���x�ᷢ����ٶ�v0=200m/s�ĵ��ӣ�����װ�÷�������У���֪��ǿ��СΪ9.3��10-7V/m����������Ϊ9.3��10-31kg������Ϊ1.6��10-19C��
��ͼ��ʾ����xOyƽ���ڣ�x���Ϸ�����y�����ϵ��㹻�����ǿ�糡���糡���±߽�Ϊy1=0.5m��ֱ�ߣ���y����y2=1.0m����һ����ԴS��x������һ���㹻����ӫ����������ԴS����ͼ180�㷶Χ�ڣ���x�ᷢ����ٶ�v0=200m/s�ĵ��ӣ�����װ�÷�������У���֪��ǿ��СΪ9.3��10-7V/m����������Ϊ9.3��10-31kg������Ϊ1.6��10-19C��