题目内容
7. 一列简谐横波沿x轴正方向传播,某时刻的波形图如图所示,从该时刻开始计时.
一列简谐横波沿x轴正方向传播,某时刻的波形图如图所示,从该时刻开始计时.①若质点P(坐标为x=3.2m)经0.4s第一次回答初始位置,求该机械波的波速和周期?
②若质点Q(坐标为x=5m)在0.5s内通过的路程为(10+5$\sqrt{2}$)cm,则该机械波的波速和周期分别是多少?
分析 (1)由波动图象可知,波长的大小;根据v=$\frac{s}{t}$,即可求解波速大小;根据波长与波速,结合$T=\frac{λ}{v}$,即可求得周期;
(2)写出该波的波动方程,确定出质点的初位置与末位置,然后即可求得波速,结合$T=\frac{λ}{v}$,即可求得周期T.
解答 解:(1)由波动图象可知,波长是8m;质点P(坐标为x=3.2m)经0.4s第一次回答初始位置,相对于O点的振动传播的P点,即该波在0.4s的时间内传播的距离是3.2m,根据v=$\frac{s}{t}$,则有简谐波的传播速度为:v=$\frac{3.2}{0.4}=8$m/s;
根据$T=\frac{λ}{v}$得:$T=\frac{8}{8}=1$s
(2)波的圆频率:$ω=\frac{2π}{T}=\frac{2πv}{λ}$,
波动方程:$y=A•sinωt=A•sin\frac{2πv}{λ}•t=A•sin\frac{2πx}{λ}$
由图可知该波的振幅是5cm,所以t=0时刻Q点的位移:${y}_{1}=5sin\frac{2π×5}{8}=-2.5\sqrt{2}$cm,
由于质点Q(坐标为x=5m)在0.5s内通过的路程为(10+5$\sqrt{2}$)cm=2A+2×$2.5\sqrt{2}$cm,可知质点Q恰好又回到了$-2.5\sqrt{2}$cm的位移处,根据波动的周期性与对称性可知,该波在0.5s的时间内,位于x=-1m处的质点的振动传播到了Q点,即该波传播的距离是:△s=5-(-1)=6m
所以:$v′=\frac{△s}{t′}=\frac{6}{0.5}m/s=12$m/s
周期:$T′=\frac{λ}{v′}=\frac{8}{12}s=\frac{2}{3}$s
答:①若质点P(坐标为x=3.2m)经0.4s第一次回答初始位置,该机械波的波速是8m/s,周期是1s;
②若质点Q(坐标为x=5m)在0.5s内通过的路程为(10+5$\sqrt{2}$)cm,则该机械波的波速是12m/s,周期是$\frac{2}{3}$s.
点评 本题关键语句在于“质点Q(坐标为x=5m)在0.5s内通过的路程为(10+5$\sqrt{2}$)cm”,需要写出波动方程,才能找到解题的突破口.审题时要善于抓住问题的突破口,并能加以分析.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 气体压强减小,单位体积内的分子数减少 | |
| B. | 气体压强降低,内能减少 | |
| C. | 气体压强增大,向外界放热 | |
| D. | 由于气体处于完全失重状态,故气体压强为零 |
 如图,光滑的四分之一圆弧轨道AB固定在竖直平面内,A端切线与水平面垂直,穿在轨道上的小球在拉力F作用下,缓慢地由A向B运动,F始终沿轨道的切线方向,轨道对球的弹力为N.在运动过程中( )
如图,光滑的四分之一圆弧轨道AB固定在竖直平面内,A端切线与水平面垂直,穿在轨道上的小球在拉力F作用下,缓慢地由A向B运动,F始终沿轨道的切线方向,轨道对球的弹力为N.在运动过程中( )| A. | F增大,N减小 | B. | F减小,N减小 | C. | F增大,N增大 | D. | F减小,N增大 |
| A. | 光由空气射入玻璃时速度变慢,波长变短 | |
| B. | 光从玻璃射入空气发生全反射时,红光的临界角小于蓝光的临界角 | |
| C. | 光学镜头上的增透膜是利用光的干涉现象 | |
| D. | 在岸边观察前方水中的一条鱼,鱼的实际深度比看到的要浅 | |
| E. | 经过同一双缝所得干涉条纹,红光条纹宽度大于绿光条纹宽度 |
 王红同学到实验室做“测定电源电动势和内阻”的实验时,发现实验桌上还有一个定值电阻R0.他设计了如图所示的电路来测量R0的阻值和电动势E和内阻r
王红同学到实验室做“测定电源电动势和内阻”的实验时,发现实验桌上还有一个定值电阻R0.他设计了如图所示的电路来测量R0的阻值和电动势E和内阻r

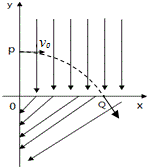 如图所示,在空间建立平面直角坐标系,在第一象限内加上电场强度大小为E、方向沿-y轴方向的匀强电场,第四象限内加上电场强度大小也为E,方向与-x轴方向成某一夹角的匀强电场.现有一质量为m、带电荷量+q的不计重力的微粒自y轴上某点P开始以初速度v0沿+x轴方向进入第一象限,微粒通过坐标为(+x0,0)的Q点后以和第四象限内的电场垂直的方向进入第四象限,不计空气阻力.求:
如图所示,在空间建立平面直角坐标系,在第一象限内加上电场强度大小为E、方向沿-y轴方向的匀强电场,第四象限内加上电场强度大小也为E,方向与-x轴方向成某一夹角的匀强电场.现有一质量为m、带电荷量+q的不计重力的微粒自y轴上某点P开始以初速度v0沿+x轴方向进入第一象限,微粒通过坐标为(+x0,0)的Q点后以和第四象限内的电场垂直的方向进入第四象限,不计空气阻力.求: 如图所示,水平长杆AB绕过B端的竖直轴OO′匀速转动,在杆上套有一个质量m=1kg的圆环,若圆环与水平杆间的动摩擦因数μ=0.5,且假设最大静摩擦力与滑动摩擦力大小相等,则:
如图所示,水平长杆AB绕过B端的竖直轴OO′匀速转动,在杆上套有一个质量m=1kg的圆环,若圆环与水平杆间的动摩擦因数μ=0.5,且假设最大静摩擦力与滑动摩擦力大小相等,则: