题目内容
3.氢原子核外电子分别在第1、2条轨道上运动时,其有关物理量的关系是( )| A. | 半径r1>r2 | B. | 电子转动角速度ω1>ω2 | ||
| C. | 电子转动向心加速度a1>a2 | D. | 总能量E1>E2 |
分析 氢原子核外电子半径rn=n2r1,能级En=$\frac{{E}_{1}}{{n}^{2}}$;向心力由静电力提供,根据牛顿第二定律求解出角速度表达式分析.
解答 解:A、氢原子核外电子半径rn=n2r1,量子数n=1、n=2对应的电子的轨道半径r1<r2,故A错误;
B、电子运动向心力F=$\frac{k{e}^{2}}{{r}^{2}}$=mω2r=ma,解得:ω=$\sqrt{\frac{k{e}^{2}}{m{r}^{3}}}$,所以F1>F2,a1>a2,ω1>ω2,故BC正确;
D、能级En=$\frac{{E}_{1}}{{n}^{2}}$,由于第一能级为负值,故量子数越大,氢原子能级越高,故D正确;
故选:BCD
点评 本题关键是熟悉波尔的氢原子模型理论的基本假设,然后结合库仑引力提供向心力列式求解角速度.

练习册系列答案
相关题目
1.理想变压器的原线圈接入表达式为i=Imsinωt的交变电流,一只灯泡和交流电流表串联后接在副线圈两端,读数为0.4A,当t=$\frac{3}{8}$T时,原线圈的电流i=30mA,由此可知,此变压器的原副线圈匝数之比为( )
| A. | 4:30 | B. | 40:3 | C. | 3:40$\sqrt{2}$ | D. | 40$\sqrt{2}$:3 |
6. 单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )
单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )
 单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )
单摆的绝缘线长1,摆球带正电,空间有匀强电场和匀强磁场,方向如图所示,若不计空气阻力,以下选项中正确的是( )| A. | 若磁场消失,仅有电场,则小球周期T>2π$\sqrt{\frac{l}{g}}$ | |
| B. | 若无电场,仅有磁场,且能保证小球正常摆动,则T>2π$\sqrt{\frac{l}{g}}$ | |
| C. | 单摆振动过程中机械能守恒 | |
| D. | 小球向右运动经过最低点时,绳的拉力最大 |
12. 如图所示的电路中,闭合开关S后,电路正常工作.某时刻,电路中某个元件出现故障,电压表、电流表的示数都变大,这可能是( )
如图所示的电路中,闭合开关S后,电路正常工作.某时刻,电路中某个元件出现故障,电压表、电流表的示数都变大,这可能是( )
 如图所示的电路中,闭合开关S后,电路正常工作.某时刻,电路中某个元件出现故障,电压表、电流表的示数都变大,这可能是( )
如图所示的电路中,闭合开关S后,电路正常工作.某时刻,电路中某个元件出现故障,电压表、电流表的示数都变大,这可能是( )| A. | 电阻R3断路 | B. | 电阻R4断路 | C. | 电阻R2短路 | D. | 电容器被击穿 |
13.关于抛体运动下列说法不正确的是( )
| A. | 抛体运动一定是曲线运动 | B. | 抛体运动一定是匀变速运动 | ||
| C. | 抛体运动可以是直线运动 | D. | 抛体运动的初速度一定不为零 |


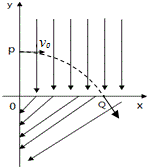 如图所示,在空间建立平面直角坐标系,在第一象限内加上电场强度大小为E、方向沿-y轴方向的匀强电场,第四象限内加上电场强度大小也为E,方向与-x轴方向成某一夹角的匀强电场.现有一质量为m、带电荷量+q的不计重力的微粒自y轴上某点P开始以初速度v0沿+x轴方向进入第一象限,微粒通过坐标为(+x0,0)的Q点后以和第四象限内的电场垂直的方向进入第四象限,不计空气阻力.求:
如图所示,在空间建立平面直角坐标系,在第一象限内加上电场强度大小为E、方向沿-y轴方向的匀强电场,第四象限内加上电场强度大小也为E,方向与-x轴方向成某一夹角的匀强电场.现有一质量为m、带电荷量+q的不计重力的微粒自y轴上某点P开始以初速度v0沿+x轴方向进入第一象限,微粒通过坐标为(+x0,0)的Q点后以和第四象限内的电场垂直的方向进入第四象限,不计空气阻力.求: