题目内容
12. 如图所示,足够大的荧光屏ON垂直于直角坐标平面xOy,且与x轴夹角为37°,当y轴与ON间有沿y轴正方向、场强为E的匀强电场时,一质量为m、电荷量为q的负离子从y轴上的P点,以速度v0、沿x轴的正方向射入电场,离子垂直打到荧光屏上的某点;现撤去电场,在y轴与ON间加上垂直坐标平面向里的匀强磁场,相同的离子仍以速度v0从y轴上的Q点也沿x轴的正方向射入磁场,离子恰好也垂直打到荧光屏上的同一点,离子的重力不计.试求:
如图所示,足够大的荧光屏ON垂直于直角坐标平面xOy,且与x轴夹角为37°,当y轴与ON间有沿y轴正方向、场强为E的匀强电场时,一质量为m、电荷量为q的负离子从y轴上的P点,以速度v0、沿x轴的正方向射入电场,离子垂直打到荧光屏上的某点;现撤去电场,在y轴与ON间加上垂直坐标平面向里的匀强磁场,相同的离子仍以速度v0从y轴上的Q点也沿x轴的正方向射入磁场,离子恰好也垂直打到荧光屏上的同一点,离子的重力不计.试求:(1)离子在电场中运动的时间t1;
(2)P点的纵坐标y1和离子在磁场中运动的加速度大小a;
(3)若相同的离子分别从y轴上的不同位置以速度v=ky(y>0,k为常数),沿x轴的正方向射入磁场,要使离子都打到荧光屏上,k应满足的条件.
分析 (1)离子在电场中做类平抛运动,应用类平抛运动规律可以求出离子的运动时间.
(2)作出离子运动轨迹,根据几何知识求出距离,由牛顿第二定律求出加速度.
(3)作出离子运动轨迹,应用牛顿第二定律求出离子的临界轨道半径,然后分析答题.
解答 解:(1)设离子垂直打到荧光屏上的M点时,沿y方向的分速度大小为vy,在电场中运动的加速度为a1,
则:${v}_{y}=\frac{{v}_{0}}{tan3{7}^{o}}$,
由牛顿第二定律得:qE=ma1,
竖直分速度:vy=a1t1,
解得:${t}_{1}=\frac{4m{v}_{0}}{qE}$;
(2)由几何关系可知:${y}_{1}=\frac{1}{2}{a}_{1}{t}_{1}^{2}+{v}_{0}{t}_{1}tan3{7}^{o}$,
解得:${y}_{1}=\frac{17m{v}_{0}^{2}}{9qE}$,
设离子在磁场中做圆周运动半径为y2,则:${y}_{2}cos3{7}^{o}={v}_{0}{t}_{1}$,
而:$a=\frac{v_0^2}{y_2}$,
解得:$a=\frac{3qE}{5m}$;
(3)如图所示,设从纵坐标为y处射入磁场的离子,
恰好能打到荧光屏上,对应的圆周运动半径为r0,
由几何知识得:
${r}_{0}+\frac{{r}_{0}}{cos3{7}^{o}}=y$
此离子进入磁场时的速度v=ky,设运动半径为r,
由牛顿第二定律得:$qBv=m\frac{v^2}{r}$,
为使离子能打到荧光屏上应满足:r≥r0,
由牛顿第二定律得:qBv0=ma,
解得:$k≥\frac{4qE}{15m{v}_{0}}$
答:(1)离子在电场中运动的时间t1为$\frac{4m{v}_{0}}{qE}$;
(2)P点距O点的距离y1为$\frac{17m{v}_{0}^{2}}{9qE}$,离子在磁场中运动的加速度大小a为$\frac{3qE}{5m}$;
(3)k应满足的条件是$k≥\frac{4qE}{15m{v}_{0}}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚离子运动过程,作出粒子运动轨迹,应用类平抛运动规律、牛顿第二定律即可正确解题,解题时要注意几何知识的应用.

 名校课堂系列答案
名校课堂系列答案| A. | 船浮于水面上 | |
| B. | 硬币或钢针浮于水面上 | |
| C. | 肥皂泡呈球形 | |
| D. | 锋利的玻璃片,用酒精灯烧一定时间后变钝了 | |
| E. | 熔化的铁水注入内空且为球形的砂箱,冷却后铸成一个铁球 |
| 金属 | 钨 | 钙 | 钠 | 钾 | 鉫 |
| W0(×10-19J) | 7.26 | 5.12 | 3.66 | 3.60 | 3.41 |
| A. | 气体的温度升高时,分子的热运动变得剧烈,分子的平均动能增大,撞击器壁时对器壁的作用力增大,从而气体的压强一定增大 | |
| B. | 气体体积变小时,单位体积的分子数增多,单位时间内打到器壁单位面积上的分子数增多,从而气体的压强一定增大 | |
| C. | 压缩一定量的气体,气体的内能一定增加 | |
| D. | 有一分子a从无穷远处趋近固定不动的分子b,当a到达受b的分子力为零处时,a具有的动能一定最大 |
| A. | 辐射光子,获得能量 | B. | 吸收光子,获得能量 | ||
| C. | 吸收光子,放出能量 | D. | 辐射光子,放出能量 |
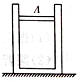 如图所示,开口向上竖直放置的内壁光滑导热良好的汽缸,内有质量为m的导热活塞,缸内密封着理想气体.初状态整个装置静止不动,气体的长度为l0=15cm,设外界大气压强为p0保持不变,温度为t0=27℃,活塞横截面积为S,且mg=p0S,求:
如图所示,开口向上竖直放置的内壁光滑导热良好的汽缸,内有质量为m的导热活塞,缸内密封着理想气体.初状态整个装置静止不动,气体的长度为l0=15cm,设外界大气压强为p0保持不变,温度为t0=27℃,活塞横截面积为S,且mg=p0S,求: 竖直平面内的半圆轨道光滑且与水平地面相切于B点,一质量为1kg的坚硬小物块A(可视为质点),静止在光滑的水平地面上,如图所示.一颗质量为10g的子弹以505m/s的速度向左飞来,正好打中并留在小物块内,它们一起向左运动,已知R=0.4m,g=10m/s2.求:
竖直平面内的半圆轨道光滑且与水平地面相切于B点,一质量为1kg的坚硬小物块A(可视为质点),静止在光滑的水平地面上,如图所示.一颗质量为10g的子弹以505m/s的速度向左飞来,正好打中并留在小物块内,它们一起向左运动,已知R=0.4m,g=10m/s2.求: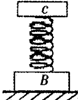 如图所示,质量为M=0.5kg的物体B和质量为m=0.2kg的物体C,用劲度系数为k=100N/m的轻弹簧连在一起.物体B放在水平地面上,物体C在轻弹簧的上方静止不动.现将物体C竖直向下缓慢压下一段距离x=0.03m后释放,物体C就上下做简谐运动,在运动过程中,物体B始终不离开地面.已知重力加速度大小为g=10m/s2.试求:当物体C运动到最高点时,物体C的加速度大小和此时物体B对地面的压力大小.
如图所示,质量为M=0.5kg的物体B和质量为m=0.2kg的物体C,用劲度系数为k=100N/m的轻弹簧连在一起.物体B放在水平地面上,物体C在轻弹簧的上方静止不动.现将物体C竖直向下缓慢压下一段距离x=0.03m后释放,物体C就上下做简谐运动,在运动过程中,物体B始终不离开地面.已知重力加速度大小为g=10m/s2.试求:当物体C运动到最高点时,物体C的加速度大小和此时物体B对地面的压力大小.