题目内容
2.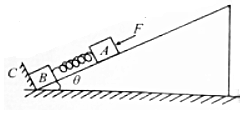 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向下的恒力F压物块A使弹簧收缩,某时刻撤除力F,物块A向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向下的恒力F压物块A使弹簧收缩,某时刻撤除力F,物块A向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )| A. | 物块B的瞬时加速度方向沿斜面向上 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A 的加速度大小为($\frac{{m}_{2}}{{m}_{1}}$+1)gsinθ | |
| D. | 物块A可能向上加速 |
分析 当B刚离开C时,弹簧的弹力等于B的重力沿斜面下的分力,根据牛顿第二定律求出物块A和B的加速度大小;根据胡克定律求解出弹簧的伸长量,结合几何关系分析.
解答 解:A、当物块B刚要离开挡板C时,弹簧的弹力等于B的重力沿斜面下的分力,物块B的瞬时加速度为零,故A错误.
B、当物块B刚要离开挡板C时,对B,根据平衡条件有 m2gsinθ=kx,由于x<d,所以有m2gsinθ<kd.故B错误.
C、当物块B刚要离开挡板C时,对A,根据牛顿第二定律得:m1gsinθ+kx2=m1aA,解得:aA=($\frac{{m}_{2}}{{m}_{1}}$+1)gsinθ,故C正确.
D、物块A的合力沿斜面向下,所以向上做减速运动,故D错误.
故选:C
点评 含有弹簧的问题,往往要研究弹簧的状态,分析物块的位移与弹簧压缩量和伸长量的关系是常用思路.

练习册系列答案
相关题目
4. 小船横渡一条两岸平行的河流,水流速度与河岸平行,船相对于水的速度大小不变,船头始终垂直指向河岸,小船的运动轨迹如图中虚线所示.则小船在此过程中( )
小船横渡一条两岸平行的河流,水流速度与河岸平行,船相对于水的速度大小不变,船头始终垂直指向河岸,小船的运动轨迹如图中虚线所示.则小船在此过程中( )
 小船横渡一条两岸平行的河流,水流速度与河岸平行,船相对于水的速度大小不变,船头始终垂直指向河岸,小船的运动轨迹如图中虚线所示.则小船在此过程中( )
小船横渡一条两岸平行的河流,水流速度与河岸平行,船相对于水的速度大小不变,船头始终垂直指向河岸,小船的运动轨迹如图中虚线所示.则小船在此过程中( )| A. | 无论水流速度是否变化,这种渡河耗时最短 | |
| B. | 越接近河中心,水流速度越小 | |
| C. | 各处的水流速度大小相同 | |
| D. | 渡河的时间随水流速度的变化而改变 |
1. 将两个内壁光滑、半径不同的半球形碗,固定在如图所示的水平台阶上,碗口在同一水平面上,取此水平面为参考平面.将两个相同的小球,分别从两个碗的边缘处无初速释放,当它们运动到各自的最低点时( )
将两个内壁光滑、半径不同的半球形碗,固定在如图所示的水平台阶上,碗口在同一水平面上,取此水平面为参考平面.将两个相同的小球,分别从两个碗的边缘处无初速释放,当它们运动到各自的最低点时( )
 将两个内壁光滑、半径不同的半球形碗,固定在如图所示的水平台阶上,碗口在同一水平面上,取此水平面为参考平面.将两个相同的小球,分别从两个碗的边缘处无初速释放,当它们运动到各自的最低点时( )
将两个内壁光滑、半径不同的半球形碗,固定在如图所示的水平台阶上,碗口在同一水平面上,取此水平面为参考平面.将两个相同的小球,分别从两个碗的边缘处无初速释放,当它们运动到各自的最低点时( )| A. | 两小球的动能相等 | B. | 两小球的动能不相等 | ||
| C. | 两小球的重力势能相等 | D. | 两小球的机械能相等 |
12.下列说法中正确的是( )
| A. | 运动是宇宙中的普遍现象,绝对不动的物体是没有的 | |
| B. | 研究物体运动时不一定要选择参考系 | |
| C. | 用GPS定位系统确定在南极冰川考察的某科考队员的位置时,该队员可看做质点 | |
| D. | 选取不同的参考系,同一物体的运动速度可能不同,但运动轨迹不变 |

 如图所示,质量为m的滑块放在光滑的水平地面上,现用一水平力缓慢向左推滑块使滑块压缩弹簧,在这程中推力做功w.撤去推力,求滑块离开弹簧时的速度v=$\sqrt{\frac{2w}{m}}$.
如图所示,质量为m的滑块放在光滑的水平地面上,现用一水平力缓慢向左推滑块使滑块压缩弹簧,在这程中推力做功w.撤去推力,求滑块离开弹簧时的速度v=$\sqrt{\frac{2w}{m}}$.
 用如图气垫导轨研究滑块A、B动量守恒,已知滑块A、B质量分别为mA、mB,滑块A、B带有宽度相同的遮光条,C、D为安装在气垫导轨上的两个光电门,实验步骤如下:
用如图气垫导轨研究滑块A、B动量守恒,已知滑块A、B质量分别为mA、mB,滑块A、B带有宽度相同的遮光条,C、D为安装在气垫导轨上的两个光电门,实验步骤如下: