题目内容
11. 用如图气垫导轨研究滑块A、B动量守恒,已知滑块A、B质量分别为mA、mB,滑块A、B带有宽度相同的遮光条,C、D为安装在气垫导轨上的两个光电门,实验步骤如下:
用如图气垫导轨研究滑块A、B动量守恒,已知滑块A、B质量分别为mA、mB,滑块A、B带有宽度相同的遮光条,C、D为安装在气垫导轨上的两个光电门,实验步骤如下:a、分别测出滑块A、B的质量mA、mB及遮光板的宽度d
b、调整气垫导轨,使导轨处于水平
c、在A和B间放入一个被压缩的轻弹簧,用电动卡销锁定,静止放置在气垫导轨上
d、按下电钮放开卡销,分别记录滑块A、B的遮光条通过光电门的时间t1、t2
(1)步骤b中,能最直观地判断导轨是否水平的方法是使滑块能静止在导轨上,或者轻推滑块后滑块做匀速运动;
(2)利用上述测量的实验数据,验证动量守恒定律的表达式是$\frac{m_{A}}{t_{1}}$=$\frac{m_{B}}{t_{2}}$;
(3)利用上述实验数据能(填“能”或“不能”)测出被压缩弹簧的弹性势能的大小,如果能请写出表达式,如果不能请说明理由Ep=$\frac{1}{2}$($\frac{{m}_{A}{d}_{\;}^{2}}{{t}_{1}^{2}}$+$\frac{{m}_{B}{d}^{2}}{{t}_{2}^{2}}$).
分析 (1)明确导轨水平时滑块的受力平衡,从而确定调节平衡的方法;
(2)根据速度公式可求得碰后两物体的速度,再根据动量守恒定律即可确定应验证的表达式;
(3)根据能量守恒,弹簧的弹性势能转化为两滑块匀速运动时的动能,求出动能的表达式即可确定被压缩弹簧的弹性势能大小.
解答 解:(1)在调整时需要接通充气开关,再调节导轨使滑块能静止在导轨上,或者轻推滑块后滑块做匀速运动,则说明导轨水平;
(2)根据速度公式可知,滑块通过光电门的速度为:vA=$\frac{d}{t_{1}}$;vB=$\frac{d}{t_{2}}$;
设向右为正方向,根据动量守恒定律可知:
mAvA-mBvB=0
代入速度并化简可得:
应满足的公式为:$\frac{m_{A}}{t_{1}}$=$\frac{m_{B}}{t_{2}}$
(3)根据功能关系是可以测出被压缩弹簧的弹性势能的大小,
根据能量守恒定律被压缩弹簧的弹性势能,有:Ep=$\frac{1}{2}$mAvA2+$\frac{1}{2}$mBvB2,
将vA=$\frac{d}{{t}_{1}}$,vB=$\frac{d}{{t}_{2}}$,代入上式得:Ep=$\frac{1}{2}$($\frac{{m}_{A}{d}_{\;}^{2}}{{t}_{1}^{2}}$+$\frac{{m}_{B}{d}^{2}}{{t}_{2}^{2}}$).
故答案为:(1)使滑块能静止在导轨上,或者轻推滑块后滑块做匀速运动;(2)$\frac{m_{A}}{t_{1}}$=$\frac{m_{B}}{t_{2}}$;(3)Ep=$\frac{1}{2}$($\frac{{m}_{A}{d}_{\;}^{2}}{{t}_{1}^{2}}$+$\frac{{m}_{B}{d}^{2}}{{t}_{2}^{2}}$).
点评 本题考查验证动量守恒定律的基本实验,理解光电门能测量瞬时速度的原理,能正确利用动量守恒定律列式,结合求出的速度即可明确应验证的表达式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案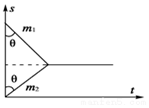 质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )
质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )| A. | 质量m1等于质量m2 | |
| B. | 碰撞前两物体动量相同 | |
| C. | 碰撞后两物体一起做匀速直线运动 | |
| D. | 碰撞前两物体动量大小相等、方向相反 |
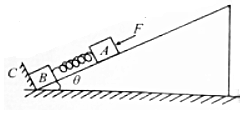 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向下的恒力F压物块A使弹簧收缩,某时刻撤除力F,物块A向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向下的恒力F压物块A使弹簧收缩,某时刻撤除力F,物块A向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )| A. | 物块B的瞬时加速度方向沿斜面向上 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A 的加速度大小为($\frac{{m}_{2}}{{m}_{1}}$+1)gsinθ | |
| D. | 物块A可能向上加速 |
| A. | 周期越来越小 | B. | 位移越来越小 | C. | 振幅越来越小 | D. | 机械能保持不变 |
| A. | 录音过程应用了“电磁感应”,放音过程应用了“电流的磁效应” | |
| B. | 录音和放音过程都应用了“电磁感应” | |
| C. | 录音过程应用了“电流的磁效应”,放音过程应用了“电磁感应” | |
| D. | 录音和放音过程都应用了“电流的磁效应” |
| A. | 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上 | |
| B. | 对于任意一个行星,其与太阳的连线在相等时间内扫过的面积相等 | |
| C. | 所有绕太阳运动的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等 | |
| D. | 所有绕太阳运动的行星的轨道的半长轴的二次方跟公转周期的三次方的比值都相等 |
 如图所示,在点电荷Q产生的电场中,实线MN是一条方向未标出的电场线,虚线AB是一个电子只在静电力作用下的运动轨迹.设电子在A、B两点的加速度大小分别为aA、aB,电势能分别为EpA、EpB.下列说法正确的是( )
如图所示,在点电荷Q产生的电场中,实线MN是一条方向未标出的电场线,虚线AB是一个电子只在静电力作用下的运动轨迹.设电子在A、B两点的加速度大小分别为aA、aB,电势能分别为EpA、EpB.下列说法正确的是( )| A. | 电子一定从A向B运动 | |
| B. | 若aA>aB,则Q靠近M端且为正电荷 | |
| C. | B点电势可能高于A点电势 | |
| D. | 无论Q为正电荷还是负电荷一定有EpA<EpB |
 如图,A、B两点分别位于大小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.以下说法正确的是( )
如图,A、B两点分别位于大小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.以下说法正确的是( )| A. | ωA=2ωC | B. | ωB=2ωA | C. | vA=vC | D. | vA=2vB |
 如图所示,质量为60kg的滑雪运动员,在倾角θ为37°的斜坡顶端,从静止开始匀加速下滑90m到达坡底,此时速度为20m/s,求运动员从斜坡顶端滑到坡底过程阻力所做的功.(sin37°=0.6,cos37°=0.8,g取10m/s2)
如图所示,质量为60kg的滑雪运动员,在倾角θ为37°的斜坡顶端,从静止开始匀加速下滑90m到达坡底,此时速度为20m/s,求运动员从斜坡顶端滑到坡底过程阻力所做的功.(sin37°=0.6,cos37°=0.8,g取10m/s2)