题目内容
3.如图所示,半径为R的光滑半圆轨道与粗糙的斜面相切于B点,斜面与水平面呈θ=37°角.质量为m=1.0kg的小物块(可视为质点),与斜面间的动摩擦因素μ=0.25,由静止从A点释放物块,到达B点进入半圆轨道时无能量损失,物块恰好能通过最高点C后离开半圆轨道.一直SAB=2m,g取10m/s2.(sin37°=0.6,cos37°=0.8)(1)求物块从A运动到B的时间t和到达B点的速度大小vB;
(2)求半圆轨道半径R;
(3)如果小物块由静止仍从A点释放,使之能沿半圆轨道返回B点,求半径R的取值范围.

分析 (1)对物块进行受力分析求得合外力,然后由牛顿第二定律求得加速度,即可根据匀变速运动规律求得运动时间和末速度;
(2)根据牛顿第二定律求得在C点的速度,然后对从B到C的运动过程应用机械能守恒求得半径;
(3)对物块从B到最高点应用机械能守恒即可求得高度,然后根据物块圆轨道返回得到半径范围.
解答 解:(1)物块在AB上运动,受到的合外力F=mgsinθ-μmgcosθ=0.2mg=2N,所以,加速度a=2m/s2;
那么由匀变速运动规律可得:物块从A运动到B的时间$t=\sqrt{\frac{2{S}_{AB}}{a}}=\sqrt{2}s$,到达B点的速度${v}_{B}=at=2\sqrt{2}m/s$;
(2)物块恰好能通过最高点C,故对物块在C点应用牛顿第二定律可得:$mg=\frac{m{{v}_{C}}^{2}}{R}$;
物块在半圆轨道上运动只有重力做功,故机械能守恒,则有:$\frac{1}{2}m{{v}_{B}}^{2}=2mgR+\frac{1}{2}m{{v}_{C}}^{2}=\frac{5}{2}mgR$,所以,$R=\frac{{{v}_{B}}^{2}}{5g}=0.16m$;
(3)小物块由静止仍从A点释放,故物块在B处的速度仍为${v}_{B}=2\sqrt{2}m/s$;
要使物块沿半圆轨道返回B点,那么物块在半圆轨道上运动能达到的最高点的竖直高度h≤R;
又有物块在半圆轨道上运动只有重力做功,机械能守恒,所以有$\frac{1}{2}m{{v}_{B}}^{2}=mgh$,所以,$R≥h=\frac{{{v}_{B}}^{2}}{2g}=0.4m$;
答:(1)物块从A运动到B的时间t为$\sqrt{2}s$;到达B点的速度大小vB为$2\sqrt{2}m/s$;
(2)半圆轨道半径R为0.16m;
(3)如果小物块由静止仍从A点释放,使之能沿半圆轨道返回B点,半径R不小于0.4m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

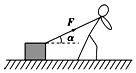 如图所示,木箱在与水平方向成α角的拉力F作用下,沿水平地面向右移动了距离l,此过程中拉力F对木箱所做的功为( )
如图所示,木箱在与水平方向成α角的拉力F作用下,沿水平地面向右移动了距离l,此过程中拉力F对木箱所做的功为( )| A. | 0 | B. | Fl | C. | Flcos α | D. | Flsin α |
| A. | 路程、力、功 | B. | 速度、加速度、动能 | ||
| C. | 位移、速度、力 | D. | 位移、时间、功率 |
| A. | 光照频率大于金属材料的逸出功 | B. | 光照频率等于金属材料的逸出功 | ||
| C. | 光照频率小于金属材料的逸出功 | D. | 光照频率与金属材料的逸出功无关 |
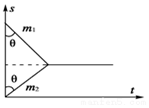 质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )
质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法中正确的是( )| A. | 质量m1等于质量m2 | |
| B. | 碰撞前两物体动量相同 | |
| C. | 碰撞后两物体一起做匀速直线运动 | |
| D. | 碰撞前两物体动量大小相等、方向相反 |
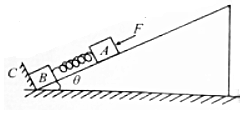 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向下的恒力F压物块A使弹簧收缩,某时刻撤除力F,物块A向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向下的恒力F压物块A使弹簧收缩,某时刻撤除力F,物块A向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )| A. | 物块B的瞬时加速度方向沿斜面向上 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A 的加速度大小为($\frac{{m}_{2}}{{m}_{1}}$+1)gsinθ | |
| D. | 物块A可能向上加速 |
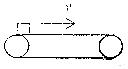 水平方向的传送带以2m/s的速度匀速运动,把一质量为2kg的小物体轻轻放在传送带上左端,经过4s物体到达传送带的右端,已知物体与传送带间的动摩擦因数为0.2,取g=10m/s2.求:
水平方向的传送带以2m/s的速度匀速运动,把一质量为2kg的小物体轻轻放在传送带上左端,经过4s物体到达传送带的右端,已知物体与传送带间的动摩擦因数为0.2,取g=10m/s2.求: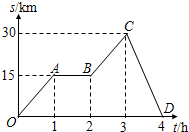 如图所示,是一辆汽车做直线运动的s-t图象,OA段表示汽车做匀速运动(填“匀速”或“变速”);AB段表示汽车处于静止状态(填“静止”或“运动”);0~1h内,汽车的位移大小是15km.
如图所示,是一辆汽车做直线运动的s-t图象,OA段表示汽车做匀速运动(填“匀速”或“变速”);AB段表示汽车处于静止状态(填“静止”或“运动”);0~1h内,汽车的位移大小是15km.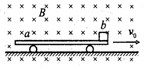 如图所示,质量M=2.0kg的小车a在光滑水平面上运动,速度为v0=13m/s,某时刻将一个质量m=0.10kg、带正电荷q=5.0×10-2C的小物体b轻轻放在小车右端.已知小车足够长且上表面粗糙,重力加速度g取10m/s2,整个空间存在水平向里、磁感应强度B=2.0T的匀强磁场,求:
如图所示,质量M=2.0kg的小车a在光滑水平面上运动,速度为v0=13m/s,某时刻将一个质量m=0.10kg、带正电荷q=5.0×10-2C的小物体b轻轻放在小车右端.已知小车足够长且上表面粗糙,重力加速度g取10m/s2,整个空间存在水平向里、磁感应强度B=2.0T的匀强磁场,求: