题目内容
1. 如图所示,在光滑斜面上有一转轴,一轻绳一端固定在转轴上,另一端拴一质量为m=1kg的小物体,轻绳能承受的最大拉力为30N.斜面倾角可以调节,随着倾角θ的变化,给小物体不同的速度,保证小物体恰好在不同倾角下都能做完整的圆周运动,g取10m/s2,则倾角θ的最大值为( )
如图所示,在光滑斜面上有一转轴,一轻绳一端固定在转轴上,另一端拴一质量为m=1kg的小物体,轻绳能承受的最大拉力为30N.斜面倾角可以调节,随着倾角θ的变化,给小物体不同的速度,保证小物体恰好在不同倾角下都能做完整的圆周运动,g取10m/s2,则倾角θ的最大值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 对小球进行受力分析,在最高点绳子拉力恰好为零时,速度取最小值,在最低点,合力提供向心力,根据向心力公式即可求解.
解答 解:小球通过最高点A的最小速度就是绳子上拉力为零的时候,所以有:
mgsinθ=m$\frac{{v}_{A}^{2}}{L}$
最高点到最低点的过程中机械能守恒,则:
$mg2Lsinθ+\frac{1}{2}m{v}_{A}^{2}=\frac{1}{2}m{v}_{B}^{2}$
小球在最低点B的最大速度满足的条件:
Fmax-mgsinθ=m$\frac{{v}_{B}^{2}}{L}$.
所以:Fmax=6mgsinθ
代入数据可得:θ=30°
故选:A
点评 本意主要考查了圆周运动向心力公式的直接应用,知道在最高点绳子拉力恰好为零时,速度取最小值,难度适中.

练习册系列答案
相关题目
11.下列说法中正确的是( )
| A. | 两物体在接触处一定有弹力作用 | B. | 两物体间存在弹力作用,一定接触 | ||
| C. | 两物体间无弹力作用,一定不接触 | D. | 两物体不接触也会有弹力作用 |
12. 如图所示,木块a和b用一根轻弹簧拴接起来,放在光滑水平面上,a紧靠在墙壁上.在b上施加向左的水平力使弹簧压缩,当撤去外力后,对a、b和弹簧组成的系统,下列说法正确的是( )
如图所示,木块a和b用一根轻弹簧拴接起来,放在光滑水平面上,a紧靠在墙壁上.在b上施加向左的水平力使弹簧压缩,当撤去外力后,对a、b和弹簧组成的系统,下列说法正确的是( )
 如图所示,木块a和b用一根轻弹簧拴接起来,放在光滑水平面上,a紧靠在墙壁上.在b上施加向左的水平力使弹簧压缩,当撤去外力后,对a、b和弹簧组成的系统,下列说法正确的是( )
如图所示,木块a和b用一根轻弹簧拴接起来,放在光滑水平面上,a紧靠在墙壁上.在b上施加向左的水平力使弹簧压缩,当撤去外力后,对a、b和弹簧组成的系统,下列说法正确的是( )| A. | a尚未离开墙壁前,系统的动量不守恒 | |
| B. | a尚未离开墙壁前,系统的机械能不守恒 | |
| C. | a离开墙后,系统的动量守恒 | |
| D. | a离开墙后,系统的机械能守恒 |
16. 如图所示,弹簧的下端固定在倾角为θ的光滑斜面底端,弹簧与斜面平行.两个完全相同的小球P、Q(均可视为质点),小球Q固定在斜面上的M点(球心在通过弹簧中心的直线ab上),小球P从斜面上的N点由静止释放,若两小球质量均为m,两小球间始终存在着大小恒定且为F的斥力,小球P从N点开始运动到第一次速度为零,运动的位移为s,则此过程( )
如图所示,弹簧的下端固定在倾角为θ的光滑斜面底端,弹簧与斜面平行.两个完全相同的小球P、Q(均可视为质点),小球Q固定在斜面上的M点(球心在通过弹簧中心的直线ab上),小球P从斜面上的N点由静止释放,若两小球质量均为m,两小球间始终存在着大小恒定且为F的斥力,小球P从N点开始运动到第一次速度为零,运动的位移为s,则此过程( )
 如图所示,弹簧的下端固定在倾角为θ的光滑斜面底端,弹簧与斜面平行.两个完全相同的小球P、Q(均可视为质点),小球Q固定在斜面上的M点(球心在通过弹簧中心的直线ab上),小球P从斜面上的N点由静止释放,若两小球质量均为m,两小球间始终存在着大小恒定且为F的斥力,小球P从N点开始运动到第一次速度为零,运动的位移为s,则此过程( )
如图所示,弹簧的下端固定在倾角为θ的光滑斜面底端,弹簧与斜面平行.两个完全相同的小球P、Q(均可视为质点),小球Q固定在斜面上的M点(球心在通过弹簧中心的直线ab上),小球P从斜面上的N点由静止释放,若两小球质量均为m,两小球间始终存在着大小恒定且为F的斥力,小球P从N点开始运动到第一次速度为零,运动的位移为s,则此过程( )| A. | 小球P的动能先增大后减小 | |
| B. | 小球P与弹簧系统的机械能先增大后减小 | |
| C. | 小球P速度最大时所受弹簧弹力大小为f=F+mgsinθ | |
| D. | 弹簧的最大弹性势能EP=FS |
6.如图所示,一小物块在水平向右的力F作用下沿光滑的固定圆柱体表面缓慢上滑,在此过程中( )
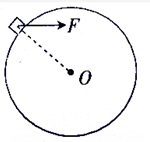

| A. | 物块受到的支持逐渐增大 | B. | 物块受到的支持力先减小后增大 | ||
| C. | 拉力F逐渐减小 | D. | 拉力F先增大后减小 |
13.(多选)用m表示地球的通讯卫星(同步卫星)的质量,h表示离地面的高度,用R表示地球的半径,g表示地球表面的重力加速度.ω表示地球自转的角速度.则通讯卫星所受的地球对它的万有引力的大小为( )
| A. | G$\frac{Mm}{(R+h)^{2}}$ | B. | $\frac{mg{R}^{2}}{(R+h)^{2}}$ | C. | mω2(R+h) | D. | m$\root{3}{{R}^{2}g{ω}^{4}}$ |
10.关于地磁场,下列说法正确的是( )
| A. | 地磁场的N极在地球的南极附近 | |
| B. | 北京地区地磁场方向由北向南 | |
| C. | 地球周围的磁感线从地球地理南极附近出发,回到地球地理北极附近 | |
| D. | 在地磁南(S)极处,可以自由转动的小磁针的N极竖直指向地面 |
 如图,光滑平行金属导轨置于水平面上,AB、CD两导体直棒相互平行横置于导轨上,匀强磁场方向竖直向上,当导体棒AB向右移动时,CD将如何运动?
如图,光滑平行金属导轨置于水平面上,AB、CD两导体直棒相互平行横置于导轨上,匀强磁场方向竖直向上,当导体棒AB向右移动时,CD将如何运动?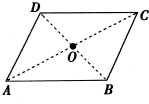 在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.
在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.