题目内容
2. 行星探测器是人类探测行星的主要工具.在某次探测过程中,探测器在靠近行星表面的轨道上做匀速圆周运动,经过t秒运动了N圈,已知该行星的半径为R,引力常量为G,求:
行星探测器是人类探测行星的主要工具.在某次探测过程中,探测器在靠近行星表面的轨道上做匀速圆周运动,经过t秒运动了N圈,已知该行星的半径为R,引力常量为G,求:(1)探测器在轨道上运动的周期T;
(2)行星的质量M;
(3)行星表面的重力加速度g.
分析 (1)根据探测器绕行星转动的圈数和时间求出探测器的周期.
(2)根据万有引力提供向心力,结合轨道半径和周期求出行星的质量.
(3)根据万有引力等于重力求出行星表面的重力加速度.
解答 解:(1)探测器在轨道上运动的周期T=$\frac{t}{N}$;
(2)根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得,行星的质量M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,
把T=$\frac{t}{N}$代入得,行星的质量M=$\frac{4{π}^{2}{N}^{2}{R}^{3}}{G{t}^{2}}$.
(3)根据万有引力等于重力得,$G\frac{Mm}{{R}^{2}}=mg$,
解得g=$\frac{GM}{{R}^{2}}$,
把M=$\frac{4{π}^{2}{N}^{2}{R}^{3}}{G{t}^{2}}$代入得,g=$\frac{4{π}^{2}{N}^{2}R}{{t}^{2}}$.
答:(1)探测器在轨道上运动的周期T为$\frac{t}{N}$;
(2)行星的质量M为$\frac{4{π}^{2}{N}^{2}{R}^{3}}{G{t}^{2}}$;
(3)行星表面的重力加速度g为$\frac{4{π}^{2}{N}^{2}R}{{t}^{2}}$.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
相关题目
13. 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于P点,轨道2、3相切于Q点如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于P点,轨道2、3相切于Q点如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于P点,轨道2、3相切于Q点如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于P点,轨道2、3相切于Q点如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )| A. | 卫星在轨道3上的速率小于在轨道1上的速率 | |
| B. | 卫星在轨道3上的角速度大于在轨道1上的角速度 | |
| C. | 卫星在轨道1具有的机械能小于它在轨道2具有的机械能 | |
| D. | 卫星在轨道2上经过Q点时的加速度等于它在轨道3上经过Q点时的加速度 |
13.下列关于热现象的说法正确的是( )
| A. | 一定质量气体压强不变温度升高时,吸收的热量一定大于内能的增加 | |
| B. | 可利用高科技手段,将流散的内能全部收集加以利用,而不引起其他变化 | |
| C. | 高空中的冰晶在空气中下落变成雨滴时,内能增加了 | |
| D. | 当分子间的相互作用力为引力时,其分子间没有斥力 | |
| E. | 布朗运动并不是分子的无规则运动,是液体分子无规则运动的反映 |
10. 让一质量为m的小球从某一高度水平抛出,小球水平抛出到落地共历时1s.设小球速度方向与水平方向夹角为θ,夹角θ的正切值tanθ随时间t变化的关系图象如图所示(g取10m/s2).下列说法正确的是( )
让一质量为m的小球从某一高度水平抛出,小球水平抛出到落地共历时1s.设小球速度方向与水平方向夹角为θ,夹角θ的正切值tanθ随时间t变化的关系图象如图所示(g取10m/s2).下列说法正确的是( )
 让一质量为m的小球从某一高度水平抛出,小球水平抛出到落地共历时1s.设小球速度方向与水平方向夹角为θ,夹角θ的正切值tanθ随时间t变化的关系图象如图所示(g取10m/s2).下列说法正确的是( )
让一质量为m的小球从某一高度水平抛出,小球水平抛出到落地共历时1s.设小球速度方向与水平方向夹角为θ,夹角θ的正切值tanθ随时间t变化的关系图象如图所示(g取10m/s2).下列说法正确的是( )| A. | 小球落地时的速度为10m/s | B. | 小球抛出点离地的高度为10m | ||
| C. | 小球水平抛出的初速度为10m/s | D. | 抛出点到落地点的距离是5$\sqrt{2}$m |
17.如图所示,在同一平面内的两颗人造卫星a、b,轨道半径之比ra:rb=2:3,下列说法正确的是( )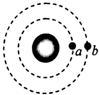

| A. | a、b线速度之比为3:2 | B. | a、b角速度之比为2$\sqrt{2}$:3$\sqrt{3}$ | ||
| C. | a、b周期之比为2$\sqrt{2}$:3$\sqrt{3}$ | D. | a、b向心加速度之比为4:9 |
14.下列说法正确的是( )
| A. | 狭义相对论的两条基本假设是相对性原理与光速不变原理 | |
| B. | 狭义相对论的两条基本假设是运动的时钟变慢与运动的尺子缩短 | |
| C. | 由于速度可以叠加,在地面测量快速运动的飞船的速度可能超过光速 | |
| D. | 任何过程所经历的时间,在不同参考系中测量都是相同的 |
 如图所示,在半径为R的光滑半圆轨道于高为10R的光滑斜轨道处于同一竖直平面内,两轨道之间用光滑轨道CD相连,水平轨道与斜轨道间有一段圆弧过渡.在水平轨道上轻弹簧被a、b两小球挤压(不栓接)处于静止状态,现同时释放两小球,a恰好能通过最高点A;b恰好能到达B点.已知a的质量为ma;b的质量为mb;求:
如图所示,在半径为R的光滑半圆轨道于高为10R的光滑斜轨道处于同一竖直平面内,两轨道之间用光滑轨道CD相连,水平轨道与斜轨道间有一段圆弧过渡.在水平轨道上轻弹簧被a、b两小球挤压(不栓接)处于静止状态,现同时释放两小球,a恰好能通过最高点A;b恰好能到达B点.已知a的质量为ma;b的质量为mb;求: