题目内容
10. 如图所示,质量为m的物体以速度v滑上水平传送带,传送带由电动机带动,始终保持以速度2v匀速运动,物体与传送带间的动摩擦因数为μ,物体最终能与传送带相对静止,重力加速度为g,对于物体从开始滑上到相对传送带静止这一过程,下列说法不正确的是( )
如图所示,质量为m的物体以速度v滑上水平传送带,传送带由电动机带动,始终保持以速度2v匀速运动,物体与传送带间的动摩擦因数为μ,物体最终能与传送带相对静止,重力加速度为g,对于物体从开始滑上到相对传送带静止这一过程,下列说法不正确的是( )| A. | 相对运动时间为$\frac{v}{μg}$ | B. | 传送带对物体做功$\frac{3m{v}^{2}}{2}$ | ||
| C. | 摩擦生热$\frac{m{v}^{2}}{2}$ | D. | 电动机做功为$\frac{5m{v}^{2}}{2}$ |
分析 物体在传送带上先做匀加速运动,后做匀速运动.由牛顿第二定律求出物体匀加速运动的加速度,由速度公式求相对运动的时间.由动能定理可求传送带对物体做功.由位移公式求出物体与传送带间的相对位移,从而得到摩擦生热.电动机做功等于物体增量和摩擦生热之和.
解答 解:A、物体做匀加速直线运动的加速度为:a=$\frac{μmg}{m}$=μg,则匀加速直线运动的时间为:t=$\frac{2v-v}{a}$=$\frac{v}{μg}$,故A正确.
B、由动能定理得:传送带对物体做功为:W=$\frac{1}{2}m(2v)^{2}$-$\frac{1}{2}m{v}^{2}$=$\frac{3m{v}^{2}}{2}$,故B正确.
C、在物体匀加速运动的这段时间内,传送带的位移为:x1=2vt=$\frac{2{v}^{2}}{μg}$,物体的位移为:x2=$\frac{v+2v}{2}t$=$\frac{3{v}^{2}}{2μg}$,则两者相对位移大小为:△x=x1-x2=$\frac{{v}^{2}}{2μg}$
则摩擦生热为:Q=μmg△x=$\frac{m{v}^{2}}{2}$.故C正确.
D、电动机做功为:W电=Q+($\frac{1}{2}m(2v)^{2}$-$\frac{1}{2}m{v}^{2}$)=2mv2,故D不正确.
本题选不正确的,故选:D
点评 解决本题的关键知道物体在传送带上发生相对运动时的运动规律,以及知道能量的转化,知道电动机做的功等于物体动能的增加和摩擦产生的内能之和.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
18.某同学沿400m的跑道跑步一圈后回到起点,此过程的路程和位移分别是( )
| A. | 400 m,0 | B. | 400 m,400 m | C. | 0,400 m | D. | 0,0 |
5.用两束频率相同,强度不同的紫外线分别照射两种相同金属的表面,均能产生光电效应,那么( )
| A. | 两束光的光子能量不同 | |
| B. | 两种情况下单位时间内逸出的光电子个数相同 | |
| C. | 两种情况下逸出的光电子的最大初动能相同 | |
| D. | 两种情况下逸出的光电子的最大初动能不同 |
2.伽利略用实验研究自由落体运动的规律,首先在斜面上做实验,这也是为了“重弹重力”,但验证v∝t时又遇到了困难,他的最大困难是( )
| A. | 不能很准确地测定下落的距离 | B. | 不能测出下落物体的瞬时速度 | ||
| C. | 当时没有测量时间的仪器 | D. | 当时没有记录落体运动的数码相机 |
19.物体做初速度为零的匀加速直线运动,第1s内的位移大小为5m,则该物体( )
| A. | 3s内位移大小为40m | B. | 1s末速度的大小为5m/s | ||
| C. | 第3s内位移大小为25m | D. | 2s末速度的大小为15m/s |
20. 如图所示,一个半径为r的半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的,一根细线跨在碗口上,线的两端分别系有可视为质点的质量为m1和m2的小球且m1=2m2,让质量为m1的小球从碗口静止释放,当其沿碗壁到达碗底时速度为v1,此时质量为 m2的小球速度为v2,则在这个过程中( )
如图所示,一个半径为r的半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的,一根细线跨在碗口上,线的两端分别系有可视为质点的质量为m1和m2的小球且m1=2m2,让质量为m1的小球从碗口静止释放,当其沿碗壁到达碗底时速度为v1,此时质量为 m2的小球速度为v2,则在这个过程中( )
 如图所示,一个半径为r的半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的,一根细线跨在碗口上,线的两端分别系有可视为质点的质量为m1和m2的小球且m1=2m2,让质量为m1的小球从碗口静止释放,当其沿碗壁到达碗底时速度为v1,此时质量为 m2的小球速度为v2,则在这个过程中( )
如图所示,一个半径为r的半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的,一根细线跨在碗口上,线的两端分别系有可视为质点的质量为m1和m2的小球且m1=2m2,让质量为m1的小球从碗口静止释放,当其沿碗壁到达碗底时速度为v1,此时质量为 m2的小球速度为v2,则在这个过程中( )| A. | 小球m1所受重力的功率一直增大 | B. | 小球m2的重力势能变化量为m2gr | ||
| C. | v2=v1sin45° | D. | v2=$\sqrt{\frac{2gr(2-\sqrt{2})}{5}}$ |
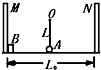 如图,绳长L=0.1m.质量为m=0.01Kg的小球和水平面接触但无相互作用,球两侧等距处放有固定挡板M、N,MN=L0=2m.现有一质量也为m=0.01Kg的小物体B靠在M挡板处,它与水平面间的摩擦因数μ=0.25.物体与小球连线垂直于挡板M、N和绳.现物体B以初速V=10m/s从挡板M处向小球A运动.物体与小球碰撞时速度变为零,小球获得物体碰前的速度,物体与挡板碰撞将以相同速率反弹回来.物体和小球均可看成质点,那么物体和小球第一次碰撞后瞬间,细绳对小球的拉力为9.6 N;物体从开始运动至最后停止的过程中,小球共转了10个整圈.(g=10m/s2)
如图,绳长L=0.1m.质量为m=0.01Kg的小球和水平面接触但无相互作用,球两侧等距处放有固定挡板M、N,MN=L0=2m.现有一质量也为m=0.01Kg的小物体B靠在M挡板处,它与水平面间的摩擦因数μ=0.25.物体与小球连线垂直于挡板M、N和绳.现物体B以初速V=10m/s从挡板M处向小球A运动.物体与小球碰撞时速度变为零,小球获得物体碰前的速度,物体与挡板碰撞将以相同速率反弹回来.物体和小球均可看成质点,那么物体和小球第一次碰撞后瞬间,细绳对小球的拉力为9.6 N;物体从开始运动至最后停止的过程中,小球共转了10个整圈.(g=10m/s2)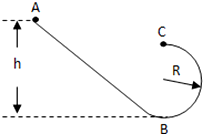 如图所示,竖直平面内的轨道由轨道AB和圆弧轨道BC组成,小球从斜面上A点由静止开始滑下,滑到斜面底端后又滑上一个半径为R的圆轨道,
如图所示,竖直平面内的轨道由轨道AB和圆弧轨道BC组成,小球从斜面上A点由静止开始滑下,滑到斜面底端后又滑上一个半径为R的圆轨道, 有两个质量分别为m1、m2的木块A、B,并列地放在光滑斜面上,如图所示.当木块A受到平行斜面向上的力F的作用时,两木块同时沿斜面向上做匀加速运动,求B木块受到的A木块的作用力大小.
有两个质量分别为m1、m2的木块A、B,并列地放在光滑斜面上,如图所示.当木块A受到平行斜面向上的力F的作用时,两木块同时沿斜面向上做匀加速运动,求B木块受到的A木块的作用力大小.