题目内容
1.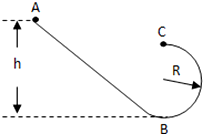 如图所示,竖直平面内的轨道由轨道AB和圆弧轨道BC组成,小球从斜面上A点由静止开始滑下,滑到斜面底端后又滑上一个半径为R的圆轨道,
如图所示,竖直平面内的轨道由轨道AB和圆弧轨道BC组成,小球从斜面上A点由静止开始滑下,滑到斜面底端后又滑上一个半径为R的圆轨道,(1)若接触面均光滑.小球刚好能滑到圆轨道的最高点C,求通过最高点C的速度
(2)若接触面均光滑.小球刚好能滑到圆轨道的最高点C,求斜面高h.
(3)若已知小球质量m=0.1kg,斜面高h=2m,轨道半径R=0.4m,小球运动到C点时对轨道压力为mg,求全过程中克服摩擦阻力做的功.取g=10m/s2.
分析 (1)小球刚好能滑到圆轨道的最高点C,在C点,由重力提供向心力,由牛顿第二定律求出小球到达C点的速度.
(2)从A到C的过程,运用机械能守恒定律求出斜面的高度h.
(3)由牛顿第二定律求出小球到达C点的速度,然后应用动能定理求出摩擦阻力做功.
解答 解:(1)小球刚好到达C点时,由重力提供向心力,由牛顿第二定律得:
mg=m$\frac{{v}_{C}^{2}}{R}$
解得 vC=$\sqrt{gR}$
(2)小球从A到C过程,由机械能守恒定律得:
mg(h-2R)=$\frac{1}{2}$mvC2,
解得:h=2.5R;
(3)在C点,由牛顿第二定律得:
mg+N=m$\frac{{v}_{C}^{′2}}{R}$
据题有 N=mg
从A到C 过程,由动能定理得:
mg(h-2R)+Wf=$\frac{1}{2}$mvC′2-0,
解得:Wf=-0.8J;
答:
(1)通过最高点C的速度是$\sqrt{gR}$.
(2)斜面高h是2.5R.
(3)全过程中克服摩擦阻力做的功是0.8J.
点评 本题是一道力学综合题,分析清楚小球的运动过程是解题的关键,要明确小球通过C点时,由合力提供向心力,应用牛顿第二定律、机械能守恒定律与动能定理可以解题,解题时要注意小球在C点做圆周运动的临界条件.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
11.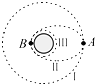 我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )
我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )
 我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )
我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )| A. | 飞船在在轨道Ⅰ上的速度大于轨道Ⅲ的速度 | |
| B. | 飞船在椭圆轨道Ⅱ上从A到B运行的过程中机械能增大 | |
| C. | 飞船在轨道Ⅲ绕月球运动一周所需的时间T=π$\sqrt{\frac{R}{{g}_{0}}}$ | |
| D. | 飞船在轨道Ⅰ上的运行速率v=$\frac{\sqrt{{g}_{0}R}}{2}$ |
12.(1)在做《探究小车速度随时间变化的规律》的实验时,要用到打点计时器,打点计时器是一种计时仪器,其电源频率为50Hz,常用的电磁打点计时器和电火花计时器使用的是交流电(直流电,交流电),它们是每隔0.02s 打一个点.
(2)接通打点计时器电源和让纸带开始运动,这两个操作之间的时间顺序关系是A
(3)小车拖动纸带运动,打出的纸带如图所示.选出A、B、C、D、E、F、G,7个计数点,每相邻两点间还有4个计时点(图中未标出).已知各点间位移.则:

①E点的瞬时速度VE=0.32m/s(保留二位有效数字);
②小车运动加速度a=0.50m/s2(保留二位有效数字).
(2)接通打点计时器电源和让纸带开始运动,这两个操作之间的时间顺序关系是A
| A.先接通电源,后让纸带运动 | B.先让纸带运动,再接通电源 |
| C.让纸带运动的同时接通电源 | D.先让纸带运动或先接通电源都可以 |

①E点的瞬时速度VE=0.32m/s(保留二位有效数字);
②小车运动加速度a=0.50m/s2(保留二位有效数字).
6.请读下面诗词:“锄禾日当午,汗滴禾下土”.在汗水下落过程中,不计空气阻力,下列说法正确的是( )
| A. | 机械能减少 | B. | 机械能增加 | C. | 重力势能减少 | D. | 重力势能增加 |
13.一个电流表的满偏电流Ig=1mA,内阻Rg=500Ω.要把它改装成一个量程为10V的电压表,则应在电流表上( )
| A. | 串联一个9.5Ω的电阻 | B. | 并联一个10 kΩ的电阻 | ||
| C. | 串联一个9.5kΩ的电阻 | D. | 并联一个9.5Ω的电阻 |
10. 如图所示,质量为m的物体以速度v滑上水平传送带,传送带由电动机带动,始终保持以速度2v匀速运动,物体与传送带间的动摩擦因数为μ,物体最终能与传送带相对静止,重力加速度为g,对于物体从开始滑上到相对传送带静止这一过程,下列说法不正确的是( )
如图所示,质量为m的物体以速度v滑上水平传送带,传送带由电动机带动,始终保持以速度2v匀速运动,物体与传送带间的动摩擦因数为μ,物体最终能与传送带相对静止,重力加速度为g,对于物体从开始滑上到相对传送带静止这一过程,下列说法不正确的是( )
 如图所示,质量为m的物体以速度v滑上水平传送带,传送带由电动机带动,始终保持以速度2v匀速运动,物体与传送带间的动摩擦因数为μ,物体最终能与传送带相对静止,重力加速度为g,对于物体从开始滑上到相对传送带静止这一过程,下列说法不正确的是( )
如图所示,质量为m的物体以速度v滑上水平传送带,传送带由电动机带动,始终保持以速度2v匀速运动,物体与传送带间的动摩擦因数为μ,物体最终能与传送带相对静止,重力加速度为g,对于物体从开始滑上到相对传送带静止这一过程,下列说法不正确的是( )| A. | 相对运动时间为$\frac{v}{μg}$ | B. | 传送带对物体做功$\frac{3m{v}^{2}}{2}$ | ||
| C. | 摩擦生热$\frac{m{v}^{2}}{2}$ | D. | 电动机做功为$\frac{5m{v}^{2}}{2}$ |
11. 如图所示的两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后释放,以悬点所在平面为参考平面,则两球经过最低点时( )
如图所示的两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后释放,以悬点所在平面为参考平面,则两球经过最低点时( )
 如图所示的两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后释放,以悬点所在平面为参考平面,则两球经过最低点时( )
如图所示的两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后释放,以悬点所在平面为参考平面,则两球经过最低点时( )| A. | 甲球的动能小于乙球的动能 | B. | 甲球的势能小于乙球的势能 | ||
| C. | 甲球的机械能小于乙球的机械能 | D. | 甲球的机械能等于乙球的机械能 |
