题目内容
11.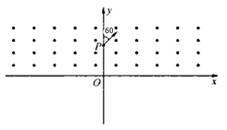 如图所示,在xoy平面内y>0的区域中存在垂直于纸面向外的匀强磁场,磁感应强度大小为B0,在y<0的区域也存在垂直纸面向外的匀强磁场(图中未画出),一带正电的粒子从y轴上的P点垂直磁场射入,速度方向与y轴正向成60°.粒子第一次进入y<0的区域时速度方向与x轴正向成150°,再次在y>0的区域运动时轨迹恰与y轴相切.已知OP的距离为2$\sqrt{3}$a,粒子的重力不计,求:
如图所示,在xoy平面内y>0的区域中存在垂直于纸面向外的匀强磁场,磁感应强度大小为B0,在y<0的区域也存在垂直纸面向外的匀强磁场(图中未画出),一带正电的粒子从y轴上的P点垂直磁场射入,速度方向与y轴正向成60°.粒子第一次进入y<0的区域时速度方向与x轴正向成150°,再次在y>0的区域运动时轨迹恰与y轴相切.已知OP的距离为2$\sqrt{3}$a,粒子的重力不计,求:(1)y<0的区域内磁场的磁感应强度大小;
(2)粒子第2n(n∈N+)次通过x轴时离O点的距离.
分析 (1)若粒子在y>0区域通过y轴时的速度方向沿y轴负方向,作出粒子的运动轨迹,根据几何关系求出粒子在上方磁场中做圆周运动的半径,以及在下方磁场做圆周运动的半径,根据半径之比,结合半径公式求出磁感应强度之比,从而得出y<0的区域内磁场的磁感应强度大小.若粒子在y>0区域通过y轴时的速度方向沿y轴正方向,同理求出y<0的区域内磁场的磁感应强度大小.
(2)根据几何关系求出粒子第2n(n∈N+)次通过x轴时离O点的距离.
解答 解:(1)由$\overline{OP}=2\sqrt{3}a$得直径为:$\overline{PQ}=\frac{\overline{OP}}{cos30°}=\frac{2\sqrt{3}a}{\frac{\sqrt{3}}{2}}=4a$,
则在上方圆周运动的半径为:${R}_{0}=\frac{1}{2}\overline{PQ}=2a$,
若粒子在y>0区域通过y轴时的速度方向沿y轴负方向,
设粒子在y<0的区域运动轨迹半径为R1,由几何关系有:
${R}_{1}=\overline{MQ}=\overline{PO}tan30°+{R}_{0}+{R}_{0}cos60°$,
解得:R1=5a.
由$R=\frac{mv}{qB}$得:$\frac{{R}_{1}}{{R}_{0}}=\frac{{B}_{0}}{{B}_{1}}$,
解得:${B}_{1}=\frac{2}{5}{B}_{0}$.
若粒子在y>0区域通过y轴时速度方向沿y轴正方向,
依据几何关系有:$\overline{{O}_{2}N}$-R0cos60°$+{R}_{2}=\overline{QO}$
解得:R2=a.
由R=$\frac{mv}{qB}$得:$\frac{{R}_{2}}{{R}_{0}}=\frac{{B}_{0}}{{B}_{2}}$,
解得:B2=2B0.
(2)粒子在y>0区域通过y轴时速度方向沿y轴负方向情况:
S1=$n(\overline{MQ}-\overline{OQ})$=3an,(n∈N+)
粒子在y>0区域通过y轴时速度方向沿y轴正方向情况:
S2=$n(\overline{OQ}-\overline{SQ})$=na,(n∈N+)
答:(1)y<0的区域内磁场的磁感应强度大小为$\frac{2}{5}{B}_{0}$或2B0;
(2)粒子第2n(n∈N+)次通过x轴时离O点的距离为S1=$n(\overline{MQ}-\overline{OQ})$=3an,(n∈N+)或S2=$n(\overline{OQ}-\overline{SQ})$=na,(n∈N+).
点评 考查了带电离子在磁场中的运动,根据题意作出粒子的运动轨迹是正确解题的前提与关键,应用几何知识与牛顿第二定律即可正确解题,注意多解问题.

| A. | 2.0×107kg/m3 | B. | 5.6×103kg/m3 | C. | 2.1×103kg/m3 | D. | 3.0×104kg/m3 |
| A. | 该古木的年代距今约5700年 | |
| B. | 12C、13C、14C具有相同的中子数 | |
| C. | 14C衰变为14N的过程中放出β射线 | |
| D. | 增加样品测量环境的压强将加速14C的衰变 |
| A. | 航天员处于失重状态 | |
| B. | 航天员处于超重状态 | |
| C. | 天宫二号比同步卫星绕地球运行的速率小 | |
| D. | 天宫二号比同步卫星绕地球运行的周期小 |
| A. | r1>r2 | |
| B. | r1<r2 | |
| C. | 相距r1时的引力大于相距r2时的引力 | |
| D. | 相距r1时的斥力大于相距r2时的斥力 |
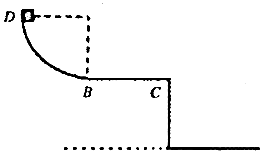 如图所示,半径为R的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B 与长为L的水平桌面相切于B点,BC离地面高为h,可视为质点的质量为m的滑块从圆 弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ,重力加速度为g,求:
如图所示,半径为R的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B 与长为L的水平桌面相切于B点,BC离地面高为h,可视为质点的质量为m的滑块从圆 弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ,重力加速度为g,求: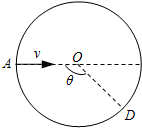 竖直平面(纸面)内有一半径为R的圆形区域,O为圆心,如图所示.在该圆形区域内加一竖直方向的匀强电场,一质量为m、电荷量为q的带正电的粒子沿图中水平直径AO从圆上的A点以速度v射入圆形区域,在圆上的D点离开该区域,已知图中θ=120°.现将电场换为充满该区域垂直纸面的匀强磁场,同一粒子以同样速度沿直径从A点射入圆形区域,也在D点离开该区域.不计粒子重力.
竖直平面(纸面)内有一半径为R的圆形区域,O为圆心,如图所示.在该圆形区域内加一竖直方向的匀强电场,一质量为m、电荷量为q的带正电的粒子沿图中水平直径AO从圆上的A点以速度v射入圆形区域,在圆上的D点离开该区域,已知图中θ=120°.现将电场换为充满该区域垂直纸面的匀强磁场,同一粒子以同样速度沿直径从A点射入圆形区域,也在D点离开该区域.不计粒子重力.
