题目内容
5.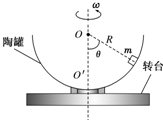 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.(1)若ω=ω0,小物块受到的摩擦力恰好为零,求ω0;
(2)若ω=2ω0,求小物块受到的摩擦力的大小和方向.
分析 (1)小物块受到的摩擦力恰好为零,靠重力和支持力的合力提供向心力,根据牛顿第二定律求出角速度的大小;
(2)当角速度为2ω时,重力和支持力的合力不够提供向心力,摩擦力方向沿罐壁切线向下,根据牛顿第二定律求出摩擦力的大小.
解答 解:(1)当摩擦力为零,支持力和重力的合力提供向心力,有:
mgtan$θ=mRsinθ{{ω}_{0}}^{2}$,
解得
${ω_0}=\sqrt{\frac{2g}{R}}$
(2)当角速度增大时,滑块有沿斜面向上滑的趋势,摩擦力沿罐壁切线向下,受力如下图所示.
Ncosθ-fsinθ-mg=0
Nsinθ+fcosθ=mr(2ω)2
联立得:f=3mgsinθ=$3mg\sqrt{1-\frac{{g}^{2}}{{R}^{2}{ω}^{4}}}$.
答:(1)小物块受到的摩擦力恰好为零时,${ω}_{0}=\sqrt{\frac{2g}{R}}$.
(2)若ω=2ω0,小物块受到的摩擦力的大小为$3mg\sqrt{1-\frac{{g}^{2}}{{R}^{2}{ω}^{4}}}$,方向沿圆弧的切线向下.
点评 解决本题的关键搞清物块做圆周运动向心力的来源,结合牛顿第二定律,抓住竖直方向上合力为零,水平方向上的合力提供向心力进行求解.

练习册系列答案
相关题目
16.关于地球的第一宇宙速度,下面说法
①它是卫星环绕地球运行的最小速度
②它是在地面上发射人造地球卫星的最小发射速度
③它卫星环绕地球运行的最大速度
④它是在地面上发射人造地球卫星的最大发射速度.
以上说法中正确的有( )
①它是卫星环绕地球运行的最小速度
②它是在地面上发射人造地球卫星的最小发射速度
③它卫星环绕地球运行的最大速度
④它是在地面上发射人造地球卫星的最大发射速度.
以上说法中正确的有( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
13.一小船渡河,河宽d=150m,水流速度v1=3m/s,船在静水中的速度v2=5m/s,则下列正确的是( )
| A. | 渡河的最短时间为t=30s | |
| B. | 渡河的最小位移为d=150m | |
| C. | 以最小位移过河时,船头与上游河岸之间的夹角为37° | |
| D. | 船不可能垂直到达正对岸 |
20. 如图所示,在水平地面上做匀速直线运动的汽车,通定滑轮用绳子吊起一个物体,若汽车和被吊物体在同一时刻的速度别为v1和v2,则下面说法正确的是( )
如图所示,在水平地面上做匀速直线运动的汽车,通定滑轮用绳子吊起一个物体,若汽车和被吊物体在同一时刻的速度别为v1和v2,则下面说法正确的是( )
 如图所示,在水平地面上做匀速直线运动的汽车,通定滑轮用绳子吊起一个物体,若汽车和被吊物体在同一时刻的速度别为v1和v2,则下面说法正确的是( )
如图所示,在水平地面上做匀速直线运动的汽车,通定滑轮用绳子吊起一个物体,若汽车和被吊物体在同一时刻的速度别为v1和v2,则下面说法正确的是( )| A. | 物体做减速运动 | B. | 物体做加速运动 | C. | v1<v2 | D. | v1>v2 |
10.下列关于静摩擦力的说法中错误的是( )
| A. | 两个相对静止物体间不一定有静摩擦力作用 | |
| B. | 受静摩擦力作用的物体一定是静止的 | |
| C. | 静摩擦力对物体总是阻力 | |
| D. | 静摩擦力一定比滑动摩擦力大 |
17.下列运动的物体,机械能守恒的是( )
| A. | 跳伞运动员在空中匀速下落 | |
| B. | 子弹射穿木块 | |
| C. | 圆锥摆球在水平面内做匀速圆周运动 | |
| D. | 物体沿竖直面内的圆形轨道做匀速圆周运动 |
15. 如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )
如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )
 如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )
如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )| A. | 迅速向下拉动活塞,缸内气体温度降低 | |
| B. | 当活塞向下移动时,外界一定对气体做正功 | |
| C. | 若汽缸导热良好,保持环境温度不变,缓慢增加重物的质量,气体一定会吸热 | |
| D. | 缓慢增加重物的质量,欲保持气体体积不变,必须设法减少气体的内能 | |
| E. | 环境温度升高,气体的压强一定增大 |
 如图所示,气缸内用两个活塞封闭两段质量、长度相同的气柱A、B,活塞可以在气缸内无摩擦地移动,活塞的厚度不计,截面积为S,每段气柱的长为L,大气压强恒为p0,温度为T0.
如图所示,气缸内用两个活塞封闭两段质量、长度相同的气柱A、B,活塞可以在气缸内无摩擦地移动,活塞的厚度不计,截面积为S,每段气柱的长为L,大气压强恒为p0,温度为T0.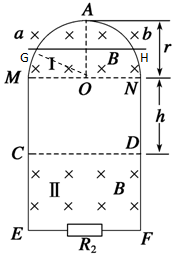 如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落r/2时的速度大小为v1,下落到MN处时的速度大小为v2.
如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落r/2时的速度大小为v1,下落到MN处时的速度大小为v2.