题目内容
15. 如图所示,气缸内用两个活塞封闭两段质量、长度相同的气柱A、B,活塞可以在气缸内无摩擦地移动,活塞的厚度不计,截面积为S,每段气柱的长为L,大气压强恒为p0,温度为T0.
如图所示,气缸内用两个活塞封闭两段质量、长度相同的气柱A、B,活塞可以在气缸内无摩擦地移动,活塞的厚度不计,截面积为S,每段气柱的长为L,大气压强恒为p0,温度为T0.①在活塞M缓慢推动$\frac{L}{2}$到虚线PQ位置时,若推力F做功为W,则A部分气体对活塞N做功为多少?
②若要保持N板不动,需要将B部分的气体温度持续升高到多少?
分析 ①气体发生等温变化,根据玻意耳定律可以求出最终气体的长度,然后应用功的公式求出做功;
②A中气体发生等温变化,应用玻意耳定律可以求出气体的压强,B部分气体发生等容变化,应用查理定律可以求出气体的温度.
解答 解:①在用力缓慢推活塞M的过程中,活塞M移动的距离为$\frac{1}{2}$L,
由于两段气体完全相同,且都发生等温变化,因此最终两段气体的长度均为$\frac{3}{4}$L,
大气压及推力对M做的总功:W总=W+p0S×$\frac{1}{2}$L=W+$\frac{1}{2}$p0LS,
由于气体对活塞的压力总是等于F+p0S,且N活塞移动的位移只是M移动距离的一半,
因此A部分气体对活塞N做的功为:WA=$\frac{1}{2}$W总=$\frac{1}{2}$W+$\frac{1}{4}$p0SL;
②如果保持N板不动,则A中气体发生等温变化,
由玻意耳定律得:p0SL=p1S×$\frac{1}{2}$L,解得:p1=2p0,
B中气体发生等容变化,由查理定律得:
$\frac{{p}_{0}SL}{{T}_{0}}$=$\frac{{p}_{1}SL}{{T}_{1}}$,解得:T1=2T0;
答:①在活塞M缓慢推动$\frac{L}{2}$到虚线PQ位置时,若推力F做功为W,则A部门气体对活塞N做功为:$\frac{1}{2}$W+$\frac{1}{4}$p0SL;
②若要保持N板不动,需要将B部分的气体温度持续升高到2T0.
点评 本题考查了求功与温度问题,分析清楚气体状态变化过程是解题的前提与关键,应用玻意耳定律、查理定律即可解题.解题时要注意两部分气体间的关系.

练习册系列答案
相关题目
3.2015年是爱因斯坦的广义相对论诞生100周年.广义相对论预言了黑洞、引力波、参考系拖拽…等各种不可思议的天文现象,这些在当时乃至其后的很长一段时间内都被认为是不可能的现象被逐一发现,更加印证了广义相对论理论的伟大.北京时间2016年2月11日23:40左右,激光干涉引力波天文台(LIGO)负责人宣布,人类首次发现了引力波.它来源于距地球之外13亿光年的两个黑洞(质量分别为26个和39个太阳质量)互相绕转最后合并的过程.合并前两个黑洞互相绕转形成一个双星系统,关于此双星系统,下列说法正确的是( )
| A. | 两个黑洞绕行的角速度相等 | B. | 两个黑洞绕行的线速度相等 | ||
| C. | 两个黑洞绕行的向心加速度相等 | D. | 质量大的黑洞旋转半径大 |
10.天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,引力常量为G,由此可求出这个双星系统的总质量为( )
| A. | $\frac{4{π}^{2}{r}^{2}(r-{r}_{1})}{G{T}^{2}}$ | B. | $\frac{4{π}^{2}{{r}_{1}}^{3}}{G{T}^{2}}$ | C. | $\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | D. | $\frac{4{π}^{2}{r}^{2}{r}_{1}}{G{T}^{2}}$ |
20.将一小球水平抛出做平抛运动,经t时间落地,若小球抛出后运动$\frac{\sqrt{2}}{2}$t时间的位移刚好是运动t时间位移的$\frac{\sqrt{3}}{3}$倍,重力加速度为g,则小球被抛出时的初速度大小为( )
| A. | $\sqrt{2}$gt | B. | $\frac{1}{2}$gt | C. | $\frac{\sqrt{2}}{2}$gt | D. | $\frac{\sqrt{2}}{4}$gt |
7.许多科学家在物理学发展中做出了重要贡献,下列表述中正确的是( )
| A. | 安培提出了磁场对运动电荷的作用力的公式 | |
| B. | 奥斯特总结并确认了真空中两个静止点电荷之间的相互作用规律 | |
| C. | 法拉第发现电磁感应现象 | |
| D. | 牛顿测出万有引力常量 |

 如图所示,分界面的上、下两侧是匀强磁场,磁感应强度大小为B,方向相反.一个质量为m、电量为+q的粒子以速度V由P点沿与界面成30°角方向射入上边的匀强磁场,不计粒子的重力,则:
如图所示,分界面的上、下两侧是匀强磁场,磁感应强度大小为B,方向相反.一个质量为m、电量为+q的粒子以速度V由P点沿与界面成30°角方向射入上边的匀强磁场,不计粒子的重力,则: 质量为2kg的物体,从竖直平面内高h=2.0m的光滑弧形轨道A处静止沿轨道滑下,并进入水平BC轨道滑行s=8.0m后停下来,取g=10m/s2,如图所示.求:
质量为2kg的物体,从竖直平面内高h=2.0m的光滑弧形轨道A处静止沿轨道滑下,并进入水平BC轨道滑行s=8.0m后停下来,取g=10m/s2,如图所示.求: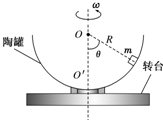 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.