题目内容
14. 如图所示,倾角为θ的光滑斜面固定在水平面上,水平虚线L下方有垂直于斜面向下的匀强磁场,磁感应强度为B.正方形闭合金属线框边长为h,质量为m,电阻为R,放置于L上方一定距离处,保持线框底边ab与L平行并由静止释放,当ab边到达L时,线框速度为v0.ab边到达L下方距离d处时,线框速度也为v0,已知d>h.以下说法正确的是( )
如图所示,倾角为θ的光滑斜面固定在水平面上,水平虚线L下方有垂直于斜面向下的匀强磁场,磁感应强度为B.正方形闭合金属线框边长为h,质量为m,电阻为R,放置于L上方一定距离处,保持线框底边ab与L平行并由静止释放,当ab边到达L时,线框速度为v0.ab边到达L下方距离d处时,线框速度也为v0,已知d>h.以下说法正确的是( )| A. | ab边刚进入磁场时,电流方向为b→a | |
| B. | ab边刚进入磁场时,线框加速度沿斜面向下 | |
| C. | 线框进入磁场过程中的最小速度小于$\frac{mgRsinθ}{{B}^{2}{h}^{2}}$ | |
| D. | 线框进入磁场过程中产生的热量为mgdsin θ |
分析 根据右手定则判断出ab边刚进入磁场时,电流的方向;当ab边到达L时,线框速度为v0.ab边到达L下方距离d处时,线框速度也为v0,知线框进入磁场时做减速运动,完全进入磁场后做加速运动.当线框完全进入磁场时,速度最小,根据能量守恒定律求出线框进入磁场过程中产生的热量.
解答 解:A、根据右手定则知,ab边刚进入磁场时,电流方向为a→b.故A错误.
B、当ab边到达L时,线框速度为v0.ab边到达L下方距离d处时,线框速度也为v0,知线框进入磁场时做减速运动,完全进入磁场后做加速运动,则ab边刚进入磁场时,做减速运动,加速度方向向上.故B错误.
C、线框从进入磁场到完全进入的过程中,做减速运动,完全进入的瞬间速度最小,此时安培力大于重力沿斜面方向的分力,根据E=BIh,I=$\frac{Bhv}{R}$,FA=BIL,根据FA>mgsinθ,有$\frac{{B}^{2}{h}^{2}v}{R}$>mgsinθ,解得v>$\frac{mgRsinθ}{{B}^{2}{h}^{2}}$.故C错误.
D、对线框进入磁场的过程运用能量守恒定律得:Q=mgdsinθ,故D正确.
故选:D.
点评 本题综合考查了右手定则、安培力大小公式、闭合电路欧姆定律、切割产生的感应电动势公式和能量守恒,知道线框进入磁场的运动规律是解决本题的关键.

练习册系列答案
相关题目
2. 如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )
如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )
 如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )
如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )| A. | 金属棒所受各力的合力所做的功为零 | |
| B. | 金属棒所受各力的合力所做的功等于mgh和电阻R上产生的焦耳热之和 | |
| C. | 恒力F与重力的合力所做的功等于棒克服安培力所做的功与电阻R上产生的焦耳热之和 | |
| D. | 恒力F与重力的合力所做的功等于电阻R上产生的焦耳热 |
9.两质量相同的卫星绕地球做匀速圆周运动,轨道半径之比r1:r2=2:1,则关于两卫星的下列说法正确的是( )
| A. | 向心加速度之比为a1:a2=1:4 | B. | 角速度之比为ω1:ω2=2:1 | ||
| C. | 动能之比为${E}_{{k}_{1}}$:${E}_{{k}_{2}}$=2:1 | D. | 机械能之比为E1:E2=1:1 |
3. 如图所示,在直线电流附近有一根金属棒ab,当金属棒以b端为圆心,以ab为半径,在过导线的平面内按图示方向匀速旋转的过程中( )
如图所示,在直线电流附近有一根金属棒ab,当金属棒以b端为圆心,以ab为半径,在过导线的平面内按图示方向匀速旋转的过程中( )
 如图所示,在直线电流附近有一根金属棒ab,当金属棒以b端为圆心,以ab为半径,在过导线的平面内按图示方向匀速旋转的过程中( )
如图所示,在直线电流附近有一根金属棒ab,当金属棒以b端为圆心,以ab为半径,在过导线的平面内按图示方向匀速旋转的过程中( )| A. | a端聚积电子 | B. | b端聚积电子 | ||
| C. | 金属棒内电场强度等于零 | D. | ua<ub |
 如图甲所示,表面绝缘、倾角θ=30°的斜面固定在水平地面上,斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形金属框abcd,放在斜面的底端,其中ab边与斜面底边重合,ab边长L=0.50m.从t=0时刻开始,线框在垂直cd边沿斜面向上大小恒定的拉力作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力,线框继续向上运动,线框向上运动过程中速度与时间的关系如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,重力加速度g取10m/s2.求:
如图甲所示,表面绝缘、倾角θ=30°的斜面固定在水平地面上,斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形金属框abcd,放在斜面的底端,其中ab边与斜面底边重合,ab边长L=0.50m.从t=0时刻开始,线框在垂直cd边沿斜面向上大小恒定的拉力作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力,线框继续向上运动,线框向上运动过程中速度与时间的关系如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,重力加速度g取10m/s2.求: 如图甲所示,两根足够长的平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B,金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g,现闭合开关S,将金属棒由静止释放.
如图甲所示,两根足够长的平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B,金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g,现闭合开关S,将金属棒由静止释放.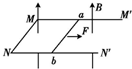 如图所示,电阻不计且足够长的U形金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数为μ,框架的宽度为L、质量为m1;质量为m2、电阻为R的均匀导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B.现对导体棒施加一水平恒力F,使棒从静止开始无摩擦地运动,当棒的运动速度达到某值时,框架开始运动.棒与框架接触良好,框架与水平面间的最大静摩擦力与滑动摩擦力相等,重力加速度为g.
如图所示,电阻不计且足够长的U形金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数为μ,框架的宽度为L、质量为m1;质量为m2、电阻为R的均匀导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B.现对导体棒施加一水平恒力F,使棒从静止开始无摩擦地运动,当棒的运动速度达到某值时,框架开始运动.棒与框架接触良好,框架与水平面间的最大静摩擦力与滑动摩擦力相等,重力加速度为g. 如图所示,cd、ef是两根电阻不计的光滑金属导轨,导轨间距离为L=0.5m,导轨所在的平面与水平面间的夹角为60°,两导轨间有垂直于导轨平面向上的匀强磁场,磁感应强度为B=0.5T,ab是质量为m=10g,电阻R=5Ω的金属棒,导轨足够长,问:
如图所示,cd、ef是两根电阻不计的光滑金属导轨,导轨间距离为L=0.5m,导轨所在的平面与水平面间的夹角为60°,两导轨间有垂直于导轨平面向上的匀强磁场,磁感应强度为B=0.5T,ab是质量为m=10g,电阻R=5Ω的金属棒,导轨足够长,问: 如图所示,在xOy竖直平面内,Y轴的右侧有垂直纸面向外的匀强磁场B=0.4T和竖直向上的匀强电场E=2N/C,长为L=16m水平绝缘传送带AB以速度v0=3m/s顺时针匀速转动,右侧轮的轴心在Y轴上,右侧轮的上侧边缘B点的坐标是(0,y=8m)一个质量为M=2g、电荷量为q=+0.01C的小物块(可视为点电荷)以轻轻放在传送带左端,小物块与传送带之间的动摩擦因数μ=0.2,小物块从传送带滑下后,经过x轴上的P点(没画出),重力加速度g=10m/s2.求:
如图所示,在xOy竖直平面内,Y轴的右侧有垂直纸面向外的匀强磁场B=0.4T和竖直向上的匀强电场E=2N/C,长为L=16m水平绝缘传送带AB以速度v0=3m/s顺时针匀速转动,右侧轮的轴心在Y轴上,右侧轮的上侧边缘B点的坐标是(0,y=8m)一个质量为M=2g、电荷量为q=+0.01C的小物块(可视为点电荷)以轻轻放在传送带左端,小物块与传送带之间的动摩擦因数μ=0.2,小物块从传送带滑下后,经过x轴上的P点(没画出),重力加速度g=10m/s2.求: