题目内容
1. 如图所示,一根轻质直杆可绕轴O在竖直平面内无摩擦地转动,OA=2l,OB=l,质量均为m的两小球分别固定在杆的A、B两端.开始时使轻杆处于水平,然后无初速地自由释放,求:
如图所示,一根轻质直杆可绕轴O在竖直平面内无摩擦地转动,OA=2l,OB=l,质量均为m的两小球分别固定在杆的A、B两端.开始时使轻杆处于水平,然后无初速地自由释放,求:(1)轻杆转到竖直位置时A、B端小球的速率
(2)轻杆由水平转到竖直位置的过程中对A、B球分别作多少功?(取重力加速度为g)
分析 (1)因A、B两球共轴转动,故两球转动的角速度相等,对A、B两球组成的系统应用机械能守恒定律即可求得小球的速率.
(2)分别对A、B两球运用动能定理列式,可求得轻杆对A、B球做功的大小.
解答 解:(1)设轻杆转到竖直位置时A、B端小球的速率分别为vA和vB.
由于A、B两球转动的角速度相等,故由v=ωr得 vA=2vB;
对A、B两球组成的系统,应用机械能守恒定律,得
mg•2l-mgl=$\frac{1}{2}$mvA2+$\frac{1}{2}$mvB2
联立以上两式解得:vA=2$\sqrt{\frac{2gl}{5}}$,vB=$\sqrt{\frac{2gl}{5}}$
(2)根据动能定理得
对A有:mg•2l+WA=$\frac{1}{2}$mvA2-0,解得 WA=-$\frac{6}{5}mgl$
对B有:WB-mgl=$\frac{1}{2}$mvB2-0,解得 WB=$\frac{6}{5}mgl$
答:
(1)轻杆转到竖直位置时A、B端小球的速率分别为2$\sqrt{\frac{2gl}{5}}$和$\sqrt{\frac{2gl}{5}}$.
(2)轻杆由水平转到竖直位置的过程中对A、B球作功分别为-$\frac{6}{5}mgl$和$\frac{6}{5}mgl$.
点评 本题关键要明确A、B球机械能均不守恒,但A与B组成的系统机械能守恒,根据系统守恒定律列式求解速度.

练习册系列答案
相关题目
3.一汽艇在水速恒定的平直河流中的甲站沿直线行驶到下游的乙站后立即返问到甲站,设汽艇顺水和逆水行驶时相对静水的速率不变,若水速恒定,来回经过的总时问为t1,若河水不动,来回经过的总时间为t2,关于t1和t2的长短,正确的是( )
| A. | t1>t2 | B. | t1<t2 | C. | t1=t2 | D. | 不能确定 |
9.下列说法正确的是( )
| A. | 带电粒子只在电场力作用下运动电势能减小 | |
| B. | 静止的电荷只在电场力作用下不一定沿电场线运动 | |
| C. | 电场线越密集的地方场强越大,电势越高 | |
| D. | 只在电场力作用下运动的带电粒子电场力不一定做功 |
16.下面关于牛顿运动定律的说法中,正确的是( )
| A. | 牛顿第一定律又叫惯性定律,惯性只有在运动的物体上才会表现出来 | |
| B. | 在合外力为零的条件下,可以推导出牛顿第一定律 | |
| C. | 合外力是物体运动状态改变的原因,加速度是合外力作用在物体上的外在体现 | |
| D. | 作用力与反作用力同时产生,同时消失,作用效果相互抵消 |
6. 如图所示,一点电荷Q产生的电场中的一条电场线,A、B为电场线上的两点,一电子以某一速度沿电场线由A运动到B的过程中,电势能增加.则下列说法正确的是( )
如图所示,一点电荷Q产生的电场中的一条电场线,A、B为电场线上的两点,一电子以某一速度沿电场线由A运动到B的过程中,电势能增加.则下列说法正确的是( )
 如图所示,一点电荷Q产生的电场中的一条电场线,A、B为电场线上的两点,一电子以某一速度沿电场线由A运动到B的过程中,电势能增加.则下列说法正确的是( )
如图所示,一点电荷Q产生的电场中的一条电场线,A、B为电场线上的两点,一电子以某一速度沿电场线由A运动到B的过程中,电势能增加.则下列说法正确的是( )| A. | 电场线方向由B向A | |
| B. | 电场强度的大小EA>EB | |
| C. | 若Q为负电荷,可以判别Q在B点的右侧 | |
| D. | 若Q为正电荷,可以判别Q在B点的右侧 |
11.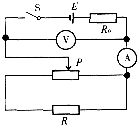 如图所示为一直流电路,电源内阻小于R0,滑动变阻器的最大阻值小于R.在滑动变阻器的滑片P从最右端滑向最左端的过程中,下列说法错误的是( )
如图所示为一直流电路,电源内阻小于R0,滑动变阻器的最大阻值小于R.在滑动变阻器的滑片P从最右端滑向最左端的过程中,下列说法错误的是( )
 如图所示为一直流电路,电源内阻小于R0,滑动变阻器的最大阻值小于R.在滑动变阻器的滑片P从最右端滑向最左端的过程中,下列说法错误的是( )
如图所示为一直流电路,电源内阻小于R0,滑动变阻器的最大阻值小于R.在滑动变阻器的滑片P从最右端滑向最左端的过程中,下列说法错误的是( )| A. | 电压表的示数一直增大 | B. | 电流表的示数一直增大 | ||
| C. | 电阻R0消耗的功率一直增大 | D. | 电源的输出功率先减小后增大 |

 如图1所示,水平地面上有一辆固定有长为L的竖直光滑绝缘管的小车,管的底部有一质量m=0.02g、电荷量q=8×10-5C的小球,小球的直径比管的内径略小.管口的侧壁处装有压力传感器,能够测出小球离开管口时对管壁的压力.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度为B1=1.5T的匀强磁场,MN面的上方还存在着竖直向上、场强E=2.5V/m的匀强电场和垂直纸面向外、磁感应强度B2=0.5T的匀强磁场.现让小车始终保持vx=2m/s的速度匀速向右运动,以带电小球刚经过场的边界PQ为计时的起点,当小球运动到管口时,测得小球对管侧壁的弹力FN=2.4×10-4N.g取10m/s2,π取3,不计空气阻力.求:
如图1所示,水平地面上有一辆固定有长为L的竖直光滑绝缘管的小车,管的底部有一质量m=0.02g、电荷量q=8×10-5C的小球,小球的直径比管的内径略小.管口的侧壁处装有压力传感器,能够测出小球离开管口时对管壁的压力.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度为B1=1.5T的匀强磁场,MN面的上方还存在着竖直向上、场强E=2.5V/m的匀强电场和垂直纸面向外、磁感应强度B2=0.5T的匀强磁场.现让小车始终保持vx=2m/s的速度匀速向右运动,以带电小球刚经过场的边界PQ为计时的起点,当小球运动到管口时,测得小球对管侧壁的弹力FN=2.4×10-4N.g取10m/s2,π取3,不计空气阻力.求: