题目内容
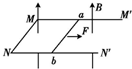
7. 金属杆MN和PQ间距为l,MP间接有电阻R,磁场如图所示,磁感应强度为B.金属棒AB长为2l,由图示位置以A为轴,以角速度ω匀速转过90°(顺时针).求该过程中(其他电阻不计):
金属杆MN和PQ间距为l,MP间接有电阻R,磁场如图所示,磁感应强度为B.金属棒AB长为2l,由图示位置以A为轴,以角速度ω匀速转过90°(顺时针).求该过程中(其他电阻不计):(1)R上的最大电流.
(2)通过R的电荷量.
分析 (1)当B转到N点时回路中有效的感应电动势最大,通过R的电流最大,功率最大.由公式E=$\frac{1}{2}$Bl2ω,求出感应电动势,再求解即可.
(2)根据法拉第电磁感应定律、欧姆定律和电流与电量的关系求解即可.
解答 解:(1)当B转到N点时回路中有效的感应电动势最大,通过R的电流最大,功率最大.
AN产生的感应电动势 E=$\frac{1}{2}$B(2l)2ω=2Bl2ω
则R上的最大功率 P=$\frac{{E}^{2}}{R}$=$\frac{4{B}^{2}{l}^{4}{ω}^{2}}{R}$
(2)在棒转过90°的过程中,AN产生的平均感应电动势
$\overline{E}$=$\frac{△Φ}{△t}$
平均电流 $\overline{I}$=$\frac{\overline{E}}{R}$
通过R的电量 q=$\overline{I}t$
磁通量的变化量△Φ=B•$\frac{1}{2}$l$\sqrt{3}$l=$\frac{\sqrt{3}B{l}^{2}}{2}$
联立以上四式得 q=$\frac{\sqrt{3}B{l}^{2}}{2R}$
答:
(1)R上的最大功率是$\frac{4{B}^{2}{l}^{4}{ω}^{2}}{R}$.
(2)通过R的电量是$\frac{\sqrt{3}B{l}^{2}}{2R}$.
点评 本题考查转动切割以及电量的计算,解题的关键要理解有效切割长度的含义,明确求电量的方法,注意掌握电量的经验公式q=$\frac{△Φ}{R}$的正确应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
2. 如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )
如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )
 如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )
如图所示,两根电阻不计的光滑平行金属导轨的倾角为θ,导轨下端接有电阻R,匀强磁场垂直于导轨平面向上.质量为m、电阻不计的金属棒ab在沿导轨平面且与棒垂直的恒力F作用下沿导轨匀速上滑,上升高度为h.在此过程中( )| A. | 金属棒所受各力的合力所做的功为零 | |
| B. | 金属棒所受各力的合力所做的功等于mgh和电阻R上产生的焦耳热之和 | |
| C. | 恒力F与重力的合力所做的功等于棒克服安培力所做的功与电阻R上产生的焦耳热之和 | |
| D. | 恒力F与重力的合力所做的功等于电阻R上产生的焦耳热 |
12. 如图所示,矩形金属框置于匀强磁场中,ef为一导体棒,可在ab和cd间滑动并接触良好.设磁感应强度为B,ac长为L,在△t时间内向左匀速滑过距离△d,由法拉第电磁感应定律E=n$\frac{△Φ}{△t}$可知,下列说法正确的是( )
如图所示,矩形金属框置于匀强磁场中,ef为一导体棒,可在ab和cd间滑动并接触良好.设磁感应强度为B,ac长为L,在△t时间内向左匀速滑过距离△d,由法拉第电磁感应定律E=n$\frac{△Φ}{△t}$可知,下列说法正确的是( )
 如图所示,矩形金属框置于匀强磁场中,ef为一导体棒,可在ab和cd间滑动并接触良好.设磁感应强度为B,ac长为L,在△t时间内向左匀速滑过距离△d,由法拉第电磁感应定律E=n$\frac{△Φ}{△t}$可知,下列说法正确的是( )
如图所示,矩形金属框置于匀强磁场中,ef为一导体棒,可在ab和cd间滑动并接触良好.设磁感应强度为B,ac长为L,在△t时间内向左匀速滑过距离△d,由法拉第电磁感应定律E=n$\frac{△Φ}{△t}$可知,下列说法正确的是( )| A. | 当ef向左滑动时,左侧面积减少L△d,右侧面积增加L△d,因此E=$\frac{2BL△d}{△t}$ | |
| B. | 当ef向左滑动时,左侧面积减少L△d,右侧面积增加L△d,互相抵消,因此E=0 | |
| C. | 在公式E=n$\frac{△Φ}{△t}$中,在切割磁感线情况下,△Φ=B△S,△S应是导体棒切割磁感线扫过的面积,因此E=$\frac{BL△d}{△t}$ | |
| D. | 在切割磁感线的情况下,只能用E=BLv计算,不能用E=n$\frac{△Φ}{△t}$计算 |
 某实验小组利用拉力传感器和速度传感器探究“外力做功与物体动能变化的关系”,如图,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连.在水平桌面上相距L的A、B两点各安装一个速度传感器.小车中放有砝码.
某实验小组利用拉力传感器和速度传感器探究“外力做功与物体动能变化的关系”,如图,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连.在水平桌面上相距L的A、B两点各安装一个速度传感器.小车中放有砝码.
 如图所示,电阻不计且足够长的U形金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数为μ,框架的宽度为L、质量为m1;质量为m2、电阻为R的均匀导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B.现对导体棒施加一水平恒力F,使棒从静止开始无摩擦地运动,当棒的运动速度达到某值时,框架开始运动.棒与框架接触良好,框架与水平面间的最大静摩擦力与滑动摩擦力相等,重力加速度为g.
如图所示,电阻不计且足够长的U形金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数为μ,框架的宽度为L、质量为m1;质量为m2、电阻为R的均匀导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B.现对导体棒施加一水平恒力F,使棒从静止开始无摩擦地运动,当棒的运动速度达到某值时,框架开始运动.棒与框架接触良好,框架与水平面间的最大静摩擦力与滑动摩擦力相等,重力加速度为g. (1)如图1所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场中.金属棒MN沿框架以速度v向右做匀速运动.框架的ab与dc平行,bc与ab、dc垂直.MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触.磁场的磁感应强度为B.
(1)如图1所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场中.金属棒MN沿框架以速度v向右做匀速运动.框架的ab与dc平行,bc与ab、dc垂直.MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触.磁场的磁感应强度为B.