题目内容
18. 半径为R的光滑半球形碗,固定于水平桌面上,一根长为L的光滑匀质棒,一端在碗内,一端在碗外,斜靠在碗缘,求平衡时棒与水平面的夹角θ.
半径为R的光滑半球形碗,固定于水平桌面上,一根长为L的光滑匀质棒,一端在碗内,一端在碗外,斜靠在碗缘,求平衡时棒与水平面的夹角θ.
分析 以杆为研究对象进行受力分析,根据水平方向受力平衡列方程,再根据力矩的平衡条件列方程,由几何关系得到碗内杆的长度,再列方程求解.
解答 解:以杆为研究对象,进行受力分析如图所示,
杆在水平方向受力平衡可得:Ncos2θ=Tsinθ①
设杆的中心为O,OB长度为x,以O点为支点,根据力矩的平衡条件可得:
N$•\frac{L}{2}$•sinθ=T•x ②
根据几何关系可得2Rcosθ=$\frac{L}{2}$+x ③
由于cosθ=cos2θ-sin2θ,
整理可得2cos2θ-$\frac{L}{4R}cosθ$-1=0,
解得:cosθ=$\frac{L}{16R}+\frac{1}{4}\sqrt{\frac{{L}^{2}}{16{R}^{2}}+8}$
所以θ=$arccos(\frac{L}{16R}+\frac{1}{4}\sqrt{\frac{{L}^{2}}{16{R}^{2}}+8})$.
答:平衡时棒与水平面的夹角θ为$arccos(\frac{L}{16R}+\frac{1}{4}\sqrt{\frac{{L}^{2}}{16{R}^{2}}+8})$.
点评 本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答.

练习册系列答案
相关题目
11.已知氦离子(He+)的能级图如图所示,根据能级跃迁理论可知( )


| A. | 氦离子(He+)从n=4能级跃迁到n=3能级比从n=3能级跃迁到n=2能级辐射出光子的频率低 | |
| B. | 大量处在n=3能级的氦离子(He+)向低能级跃迁,只能发出2种不同频率的光子 | |
| C. | 氦离子(He+)处于n=1能级时,能吸收45eV的能量跃迁到n=2能级 | |
| D. | 氦离子(He+)从n=3能级跃迁到n=2能级比从n=4能级跃迁到n=2能级辐射出的光容易衍射 |
13.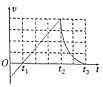 如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
 如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )| A. | t2时刻运动员到达起跳的最高点 | B. | t2~t3时间内,运动员处于失重状态 | ||
| C. | 0~t2时间内,运动员机械能守恒 | D. | 0~t3时间内,合力对运动员做负功 |
3. 如图所示,在水平面上,静止着一斜面体有一玩具小车放在斜面上刚好匀速下滑,现用平行于斜面向下的力F推小车,小车沿斜面向下做匀加速运动,斜面体仍静止不动,则( )
如图所示,在水平面上,静止着一斜面体有一玩具小车放在斜面上刚好匀速下滑,现用平行于斜面向下的力F推小车,小车沿斜面向下做匀加速运动,斜面体仍静止不动,则( )
 如图所示,在水平面上,静止着一斜面体有一玩具小车放在斜面上刚好匀速下滑,现用平行于斜面向下的力F推小车,小车沿斜面向下做匀加速运动,斜面体仍静止不动,则( )
如图所示,在水平面上,静止着一斜面体有一玩具小车放在斜面上刚好匀速下滑,现用平行于斜面向下的力F推小车,小车沿斜面向下做匀加速运动,斜面体仍静止不动,则( )| A. | 小车匀速下滑时,地面对斜面体的摩擦力方向水平向左 | |
| B. | 小车匀加速下滑时,地面对斜面体的摩擦力方向水平向左 | |
| C. | 小车匀加速下滑时,地面对斜面体的摩擦力方向水平向右 | |
| D. | 以上说法都不对 |
8.一质量不变的运动物体,速度变为原来的2倍时其动能变为原来的( )
| A. | $\frac{1}{4}$倍 | B. | $\frac{1}{2}$倍 | C. | 2倍 | D. | 4倍 |

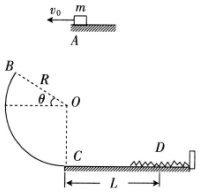 如图所示,半径R=0.4m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连 线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与粗糙水平面相切,一根轻质弹簧的右端固定在 竖直挡板上.质量m=0.1kg的小物块(可视为质点)从空中的A点以v0=2m/s的速度被水平拋出,恰好从B点沿轨道切线方向进入轨道,经过C点后沿水平面向右运动至D点时,弹簧被压缩至最短,此时弹簧的弹性势能Epm=0.8J,已知小物块与水平面间的动摩擦因数μ=0.5,g取10m/s2.求:
如图所示,半径R=0.4m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连 线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与粗糙水平面相切,一根轻质弹簧的右端固定在 竖直挡板上.质量m=0.1kg的小物块(可视为质点)从空中的A点以v0=2m/s的速度被水平拋出,恰好从B点沿轨道切线方向进入轨道,经过C点后沿水平面向右运动至D点时,弹簧被压缩至最短,此时弹簧的弹性势能Epm=0.8J,已知小物块与水平面间的动摩擦因数μ=0.5,g取10m/s2.求: 如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑的同时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=0.75m,斜面倾角θ=37°,不计空气阻力.求:
如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑的同时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=0.75m,斜面倾角θ=37°,不计空气阻力.求: