题目内容
9．对于磁场中的闭合电路，以下说法正确的是（ ）| A． | 当闭合电路做切割磁感线运动，电路中就一定有感应电流 | |
| B． | 当闭合电路静止，电路中就一定没有感应电流 | |
| C． | 只要穿过闭合电路的磁感线条数发生变化，闭合电路中就有感应电流 | |
| D． | 只要闭合电路内有磁通量，闭合电路中就有感应电流 |
分析 发生感应电流的条件是穿过闭合线圈的磁通量发生变化，或闭合线路的一部分做切割磁感线运动．根据题意逐项判断即可．
解答 解：A、当闭合电路整体做切割磁感线运动，回路中的磁通量不变，电路中就没有感应电流．故A错误；
B、当闭合电路静止，回路中的磁通量不变，电路中就一定没有感应电流；回路中的磁通量若发生变化，则有感应电流产生．故B错误；
C、发生感应电流的条件是穿过闭合线圈的磁通量发生变化．而磁感线条数可以表示磁通量；故条数发生变化时，一定有感应电流产生；故C正确；
D、发生感应电流的条件是穿过闭合线圈的磁通量发生变化．只有磁通量不一定能产生感应电流；故D错误；
故选：C．
点评 本题考查了产生感应电流的条件，根据该条件解答即可．要注意明确条件为：闭合回路中磁通量发生了变化．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
19．把一个质量为1kg的物块从某高处由静止释放，不计空气阻力，重力加速度g取10m/s2．（物体未落地）．求：
（1）前3s内重力做功的平均功率；
（2）第3s内重力做的功；
（3）第3s末重力的功率．
（1）前3s内重力做功的平均功率；
（2）第3s内重力做的功；
（3）第3s末重力的功率．
20．物体脱离星球引力所需要的最小速度称为第二宇宙速度，第二宇宙速度v2与第一宇宙速度v1的关系是v2=$\sqrt{2}$v1．已知某星球半径是地球半径R的$\frac{1}{3}$，其表面的重力加速度是地球表面重力加速度g的$\frac{1}{6}$，不计其它星球的影响，则该星球的第二宇宙速度为（ ）
| A． | $\frac{1}{6}$$\sqrt{gR}$ | B． | $\sqrt{gR}$ | C． | $\frac{1}{3}$$\sqrt{gR}$ | D． | $\sqrt{3gR}$ |
17．如图所示为一个绕中心线OO'以角速度ω转动的球，下列说法正确的是（ ）
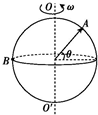
| A． | A、B两点的角速度相等 | B． | A、B两点的线速度相等 | ||
| C． | 若θ=30°，则vA：vB=1：2 | D． | 若θ=30°，则vA：vB=$\sqrt{3}$：2 |
4．
如图所示，半径为R的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度为B．M为磁场边界上一粒子发射源，可在纸面内向各个方向发射带电量为q、质量为m、速率相同的带电粒子，不计粒子重力，粒子射出磁场时的位置均处于磁场边界的某一段圆弧上，这段圆弧的弧长是磁场边界圆周长的$\frac{1}{6}$．则粒子从M点进人磁场时的速率为（ ）
如图所示，半径为R的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度为B．M为磁场边界上一粒子发射源，可在纸面内向各个方向发射带电量为q、质量为m、速率相同的带电粒子，不计粒子重力，粒子射出磁场时的位置均处于磁场边界的某一段圆弧上，这段圆弧的弧长是磁场边界圆周长的$\frac{1}{6}$．则粒子从M点进人磁场时的速率为（ ）| A． | $\frac{qBR}{2m}$ | B． | $\frac{qBR}{m}$ | C． | $\frac{\sqrt{2}qBR}{2m}$ | D． | $\frac{\sqrt{2}qBR}{m}$ |
14．
一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动．某时刻在传送带适当的位置放上具有一定初速度的物块（如图a所示），以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小v1＞v2）．已知传送带的速度保持不变．则下列判断正确的是（ ）
一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动．某时刻在传送带适当的位置放上具有一定初速度的物块（如图a所示），以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小v1＞v2）．已知传送带的速度保持不变．则下列判断正确的是（ ）| A． | 物块与传送带间的动摩擦因数为μ，μ＞tanθ | |
| B． | 0～t1内，物块对传送带做正功 | |
| C． | 0～t2内，系统产生的热量一定比物块动能的减少量大 | |
| D． | 0～t2内，传送带对物块做的功等于物块动能的减少量 |
某同学尝试把一个灵敏电流表改装成温度表，他所选用的器材有：灵敏电流表（待改装），学生电源（电动势为E，内阻不计），滑动变阻器，单刀双掷开关，导线若干，导热性能良好的防水材料，标准温度计，PTC热敏电阻Rt（PTC线性热敏电阻的阻值与摄氏旁温度t的关系为Rt=a+kt，a＞0，k＞0）．设计电路如图所示，并按如下步骤进行操作：
如图所示，绝缘轨道CDGH位于竖直平面内，圆弧段DG的圆心角为θ=37°，DG与水平段CD、倾斜段GH分别相切于D点和G点，CD段粗糙，DGH段光滑，在H处固定一垂直于轨道的绝缘挡板，整个轨道处于场强为E=1×104N/C、水平向右的匀强电场中．一质量m=4×10-3kg、带电量q=+3×10-6C的小滑块在C处由静止释放，经挡板碰撞后滑回到CD段的中点P处时速度恰好为零．已知CD段长度L=0.8m，圆弧DG的半径r=0.2m；不计滑块与挡板碰撞时的动能损失，滑块可视为质点．求：
直平行金属极板MN、PQ间存在水平向右的匀强电场，极板间距为L，A、B为PQ极板上同一竖直线上的小孔，A孔距离极板边缘距离及B孔距离均为2L，PQ极板右侧存在一垂直纸面向外的匀强磁场，如图所示，有一质量为m，带电量为+q的粒子以速度v0从MN极板上边缘竖直向下射入电场，恰好能从A孔进入磁场，并能从B孔返回电场，粒子重力及空气阻力不计，粒子不与极板发生碰撞，求：