题目内容
17.如图所示为一个绕中心线OO'以角速度ω转动的球,下列说法正确的是( )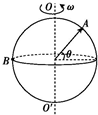
| A. | A、B两点的角速度相等 | B. | A、B两点的线速度相等 | ||
| C. | 若θ=30°,则vA:vB=1:2 | D. | 若θ=30°,则vA:vB=$\sqrt{3}$:2 |
分析 共轴转动的各点角速度相等,再根据v=rω判断线速度的大小.
解答 解:A、共轴转动的各点角速度相等,故A、B两点的角速度相等;故A正确;
B、若θ=30°,A点的转动半径为 RA=Rcos30°=0.5$\sqrt{3}$R,B点的转动半径为RB=R,根据v=ωr,则:$\frac{{v}_{A}}{{v}_{B}}=\frac{\sqrt{3}}{2}$.故B错误,C错误,D正确;
故选:AD
点评 解决本题的关键知道共轴转动各点角速度大小相等,以及知道角速度、线速度、半径之间的关系公式.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
7.关于地球自转对重力加速度的影响,下列说法中正确的是( )
| A. | 在赤道上重力加速度最大 | |
| B. | 在两极重力加速度最大 | |
| C. | 在地球上各处重力加速度都是9.8m/s2 | |
| D. | 地球的自转使物体的重力大于地球对它的引力 |
2.下面对生活的实例解释正确的是( )
| A. | 人从高处跳下落地时,总有一个曲膝的动作,是为了减少地面对人的冲量 | |
| B. | 运输玻璃时总要用些泡沫填塞,是为了减少震荡过程中的冲力 | |
| C. | 从桌子腿下抽出压着的书,为了避免桌子翻倒,应慢慢抽 | |
| D. | 从乒乓球下快速抽出一张纸条,乒乓球不动是因为乒乓球受到纸条摩擦力的冲量太小 |
9.对于磁场中的闭合电路,以下说法正确的是( )
| A. | 当闭合电路做切割磁感线运动,电路中就一定有感应电流 | |
| B. | 当闭合电路静止,电路中就一定没有感应电流 | |
| C. | 只要穿过闭合电路的磁感线条数发生变化,闭合电路中就有感应电流 | |
| D. | 只要闭合电路内有磁通量,闭合电路中就有感应电流 |
6. 我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根长度一定的轻绳OA、OB悬挂在水平天花板上,O为结点,OA>OB,∠AOB=90°.设OA、OB对O点的拉力大小分别为FA、FB,轻绳能够承受足够大的拉力,则( )
我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根长度一定的轻绳OA、OB悬挂在水平天花板上,O为结点,OA>OB,∠AOB=90°.设OA、OB对O点的拉力大小分别为FA、FB,轻绳能够承受足够大的拉力,则( )
 我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根长度一定的轻绳OA、OB悬挂在水平天花板上,O为结点,OA>OB,∠AOB=90°.设OA、OB对O点的拉力大小分别为FA、FB,轻绳能够承受足够大的拉力,则( )
我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根长度一定的轻绳OA、OB悬挂在水平天花板上,O为结点,OA>OB,∠AOB=90°.设OA、OB对O点的拉力大小分别为FA、FB,轻绳能够承受足够大的拉力,则( )| A. | FA大于FB | |
| B. | FA、FB的合力大于mg | |
| C. | 若左右调节A点位置,可使FA等于FB | |
| D. | 若左右调节A点位置,可使FA、FB均大于mg |
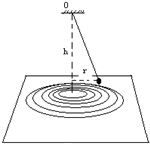 如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t.
如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t. 在“研究匀变速直线运动”的实验中,某同学在打出的纸带上按打点的先后顺序每5个点取一个计数点,共取了A、B、C、D、E、F,六个计数点(每相邻两个计数点间还有四个点).从A点开始在每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由长到短紧靠但不重叠地粘在xoy坐标系中,如图所示.
在“研究匀变速直线运动”的实验中,某同学在打出的纸带上按打点的先后顺序每5个点取一个计数点,共取了A、B、C、D、E、F,六个计数点(每相邻两个计数点间还有四个点).从A点开始在每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由长到短紧靠但不重叠地粘在xoy坐标系中,如图所示. 如图所示,人拉着绳的一端从滑轮组正下方的A处向右运动4m,使质量为20kg的重物匀速上升,如果人在A处时手到滑轮的距离为3m,滑轮的质量、大小和摩擦均不计,则在上述过程中,人拉物体所做的功是( )
如图所示,人拉着绳的一端从滑轮组正下方的A处向右运动4m,使质量为20kg的重物匀速上升,如果人在A处时手到滑轮的距离为3m,滑轮的质量、大小和摩擦均不计,则在上述过程中,人拉物体所做的功是( )