题目内容
20.物体脱离星球引力所需要的最小速度称为第二宇宙速度,第二宇宙速度v2与第一宇宙速度v1的关系是v2=$\sqrt{2}$v1.已知某星球半径是地球半径R的$\frac{1}{3}$,其表面的重力加速度是地球表面重力加速度g的$\frac{1}{6}$,不计其它星球的影响,则该星球的第二宇宙速度为( )| A. | $\frac{1}{6}$$\sqrt{gR}$ | B. | $\sqrt{gR}$ | C. | $\frac{1}{3}$$\sqrt{gR}$ | D. | $\sqrt{3gR}$ |
分析 第一宇宙速度是人造地球卫星在近地圆轨道上的运行速度,即$\frac{GMm}{{R}^{2}}$=$\frac{m{v}^{2}}{R}$,此题把地球第一宇宙速度的概念迁移的某颗星球上面,从而即可求解.
解答 解:设某星球的质量为M,半径为r,绕其飞行的卫星质量m,
由万有引力提供向心力得:$\frac{GMm}{{r}^{2}}$=$\frac{m{v}_{1}^{2}}{r}$
解得:v1=$\sqrt{\frac{GM}{r}}$①
又因它表面的重力加速度为地球表面重力加速度g的$\frac{1}{6}$.
得:$\frac{GMm}{{r}^{2}}$=m$\frac{g}{6}$ ②
且v2=$\sqrt{2}$v1 ③
由①②③解得:v2=$\sqrt{\frac{gr}{3}}$=$\frac{\sqrt{gR}}{3}$,故C正确,ABD错误;
故选:C.
点评 通过此类题型,学会知识点的迁移,比如此题:把地球第一宇宙速度的概念迁移的某颗星球上面,注意第一宇宙速度对应的轨道半径是解题的关键,及理解引力等于重力的应用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
10.关于运动的合成,下列说法正确的是( )
| A. | 合运动的速度一定比每一个分运动的速度大 | |
| B. | 两个直线运动的合运动,一定是直线运动 | |
| C. | 合运动的加速度一定比每个分运动加速度大 | |
| D. | 分运动的时间,一定与它们的合运动的时间相等 |
11.在万有引力理论发展经历中,提出万有引力定律和测出常量的科学家分别是( )
| A. | 开普勒、卡文迪许 | B. | 牛顿、伽利略 | C. | 牛顿、卡文迪许 | D. | 开普勒、伽利略 |
9.对于磁场中的闭合电路,以下说法正确的是( )
| A. | 当闭合电路做切割磁感线运动,电路中就一定有感应电流 | |
| B. | 当闭合电路静止,电路中就一定没有感应电流 | |
| C. | 只要穿过闭合电路的磁感线条数发生变化,闭合电路中就有感应电流 | |
| D. | 只要闭合电路内有磁通量,闭合电路中就有感应电流 |
10.质量为m的物体,以$\frac{4}{3}$g的加速度向上做匀减速直线运动,在上升高度h的过程中,下列说法中正确的是( )
| A. | 物体重力势能增加$\frac{4}{3}$mgh | B. | 物体的机械能减少$\frac{1}{3}$mgh | ||
| C. | 重力对物体做功-$\frac{4}{3}$mgh | D. | 物体的动能增加$\frac{4}{3}$mgh |
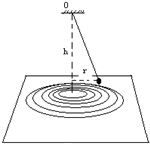 如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t.
如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t. 如图所示,滑块A的质量为m,小车B的质量为M且M=2m,滑块与平板小车之间的动摩擦因数为μ,小车静止在光滑的水平面上,当滑块以速度v0,从小车右端滑上小车,经一段时间后滑块相对小车静止,已知重力加速度为g,求:
如图所示,滑块A的质量为m,小车B的质量为M且M=2m,滑块与平板小车之间的动摩擦因数为μ,小车静止在光滑的水平面上,当滑块以速度v0,从小车右端滑上小车,经一段时间后滑块相对小车静止,已知重力加速度为g,求: 在“研究匀变速直线运动”的实验中,某同学在打出的纸带上按打点的先后顺序每5个点取一个计数点,共取了A、B、C、D、E、F,六个计数点(每相邻两个计数点间还有四个点).从A点开始在每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由长到短紧靠但不重叠地粘在xoy坐标系中,如图所示.
在“研究匀变速直线运动”的实验中,某同学在打出的纸带上按打点的先后顺序每5个点取一个计数点,共取了A、B、C、D、E、F,六个计数点(每相邻两个计数点间还有四个点).从A点开始在每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由长到短紧靠但不重叠地粘在xoy坐标系中,如图所示.