题目内容
5. 氢原子的核外电子质量为m,电量为-e,在离核最近的轨道上运动,轨道半径为r,试回答下列问题:
氢原子的核外电子质量为m,电量为-e,在离核最近的轨道上运动,轨道半径为r,试回答下列问题:(1)电子运动的动能EK是多少?
(2)电子绕核转动周期T是多少?
(3)电子绕核在如图所示的x-y平面上沿A→B→C→D方向转动,电子转动相当于环形电流,则此电流方向如何?电流强度为多大?
(4)如果沿Ox方向加一匀强磁场,则整个原子将怎样运动?
分析 (1)电子绕原子核运动,根据原子核对电子的库仑力提供向心力,由牛顿第二定律求出电子的动能;
(2)库伦力提供向心力,应用牛顿第二定律求出周期.
(3)电子绕核在如图所示xy平面上沿A→B→C→D方向转动,电子转动相当于环形电流,则此电流的方向顺时针,根据电流定义式求出电流强度.
(4)应用左手定则判断出原子所受洛伦兹力方向,根据原子所受洛伦兹力判断原子如何运动.
解答 解:(1)原子核对电子的库仑力提供向心力,由牛顿第二定律及库仑定律得:k$\frac{{e}^{2}}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,
则电子运动的动能为:Ek=$\frac{1}{2}$mv2=$\frac{k{e}^{2}}{2r}$;
(2)原子核对电子的库仑力提供向心力,由牛顿第二定律及库仑定律得:
k$\frac{{e}^{2}}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,
解得:T=$\frac{2π}{e}$$\sqrt{\frac{m{r}^{3}}{k}}$;
(3)电子绕核在如图所示xy平面上沿A→B→C→D方向转动,
电子转动相当于环形电流,则此电流的方向顺时针.
电流强度:I=$\frac{e}{T}$=$\frac{{e}^{2}}{2π}$$\sqrt{\frac{k}{m{r}^{3}}}$;
(4)根据左手定则,圆的x>0的一半,电子受磁场垂直纸面向纸面外的力,
x<0的一半,电子受到垂直纸面向内的力.因此,整个原子以Oy为轴,从Oy方向看为逆时针方向转动.
答:(1)电子运动的动能EK是$\frac{k{e}^{2}}{2r}$;
(2)电子绕核转动周期T是$\frac{2π}{e}$$\sqrt{\frac{m{r}^{3}}{k}}$;
(3)此电流方向:沿顺时针方向,电流强度为$\frac{{e}^{2}}{2π}$$\sqrt{\frac{k}{m{r}^{3}}}$;
(4)如果沿Ox方向加一匀强磁场,整个原子以Oy为轴,从Oy方向看为逆时针方向转动.
点评 沿Ox方向加一匀强磁场,原子中要受到洛伦兹力作用,应用左手定则判断原子受力时应注意研究对象的选择,从两半部分分析原子的受力,然后得出结论;在能够根据题意找出氢原子核与核外电子的库仑力提供向心力,并列出等式求解.

 走进文言文系列答案
走进文言文系列答案| A. | k$\frac{{Q}^{2}}{{r}^{2}}$ | B. | k$\frac{5{Q}^{2}}{{r}^{2}}$ | C. | k$\frac{4{Q}^{2}}{{r}^{2}}$ | D. | k$\frac{2{Q}^{2}}{{r}^{2}}$ |
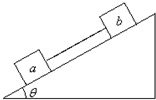 如图所示,用轻绳连接同种材料制成的a和b两个物体.a物体的质量为m1,b物体的质量为m2,m1>m2,当它们沿着有摩擦的斜面向下滑动时,连接两物体的细线的受力情况是( )
如图所示,用轻绳连接同种材料制成的a和b两个物体.a物体的质量为m1,b物体的质量为m2,m1>m2,当它们沿着有摩擦的斜面向下滑动时,连接两物体的细线的受力情况是( )| A. | 当a和b两物体匀速下滑时,细线中的拉力等于零;当a和b两物体不是匀速下滑时,细线中的拉力不等于零 | |
| B. | 当a与b两物体一起加速下滑时,b物体通过细线拉a物体向下加速运动 | |
| C. | 不论a与b是匀速运动,还是加速运动,细线中的拉力均等于零 | |
| D. | 两物体与斜面的摩擦力相等时,细线中的拉力才可能等于零 |
 如图所示,质量为1kg的物块在倾角为53°的固定斜面上向下滑动,若给物块施加平行于斜面向上的拉力F,则物块刚好能匀速下滑,F=5N.求:物块与斜面之间的动摩擦因数.(sin53°=0.8,cos53°=0.6,g=10N/kg)
如图所示,质量为1kg的物块在倾角为53°的固定斜面上向下滑动,若给物块施加平行于斜面向上的拉力F,则物块刚好能匀速下滑,F=5N.求:物块与斜面之间的动摩擦因数.(sin53°=0.8,cos53°=0.6,g=10N/kg) 如图所示,水平面上固定着一个半径R=0.4m的光滑圆环形轨道.在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B(均可看作质点),两小球间夹一轻质短弹簧(弹簧的长度相对环形轨道的半径和周长而言可忽略不计).开始时,两小球将轻质弹簧压缩,已知压缩弹簧在弹开前储存的弹性势能E=1.2J,弹簧释放后,两小球沿轨道反方向运动.
如图所示,水平面上固定着一个半径R=0.4m的光滑圆环形轨道.在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B(均可看作质点),两小球间夹一轻质短弹簧(弹簧的长度相对环形轨道的半径和周长而言可忽略不计).开始时,两小球将轻质弹簧压缩,已知压缩弹簧在弹开前储存的弹性势能E=1.2J,弹簧释放后,两小球沿轨道反方向运动.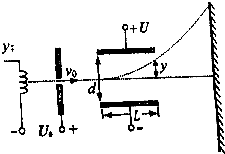 示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求:
示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求: