题目内容
10.2013年12月14日21时11分,“嫦娥三号”在月球正面的虹湾以东地区着陆,假设着陆前,“嫦娥三号”探月卫星绕月球表面匀速飞行(不计周围其他天体的影响),宇航员测出“嫦娥三号”飞行N圈用时为t,已知地球质量为M,地球半径为R,月球半径为r,地球表面重力加速度为g,则( )| A. | “嫦娥三号”探月卫星匀速飞行的速度为$\frac{2πNR}{t}$ | |
| B. | 月球的平均密度为$\frac{3πM{N}^{2}}{g{r}^{2}{t}^{2}}$ | |
| C. | “嫦娥三号”探月卫星的质量为$\frac{4{π}^{2}{N}^{2}{r}^{3}}{g{R}^{2}{t}^{2}}$ | |
| D. | “嫦娥三号”探月卫星绕月球表面匀速飞行的向心加速度为$\frac{4{π}^{2}{N}^{2}r}{{t}^{2}}$ |
分析 由T=$\frac{t}{N}$求出“嫦娥三号”探月卫星匀速飞行的周期,由T=$\frac{2πR}{v}$求解其速度.根据万有引力等于向心力,列式求出月球的质量,再求解月球的密度.
解答 解:A、“嫦娥三号”探月卫星匀速飞行的周期为 T=$\frac{t}{N}$
由T=$\frac{2πr}{v}$,得卫星匀速飞行的速度 v=$\frac{2πNr}{t}$,故A错误.
B、根据G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}r$,得月球的质量为 M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$=$\frac{4{π}^{2}{r}^{3}{N}^{2}}{G{t}^{2}}$
月球的密度 ρ=$\frac{M}{\frac{4}{3}π{r}^{3}}$=$\frac{3π{N}^{2}}{G{t}^{2}}$.故B错误.
C、由上式可知,不能解出卫星的质量,故C错误.
D、“嫦娥三号”探月卫星绕月球表面匀速飞行的向心加速度为 a=$\frac{4{π}^{2}}{{T}^{2}}r$=$\frac{4{π}^{2}{N}^{2}r}{{t}^{2}}$,故D正确.
故选:D.
点评 解决本题的关键掌握万有引力的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
20.地球表面附近某区域存在大小为1.5×102N/C、方向竖直向下的电场.将一质量为1.0×10-4kg、带电量为+1.0×10-7C的小球由静止释放,则该小球在此区域内下落10m的过程中,其电势能和动能的变化情况为(不计空气阻力,重力加速度g=10m/s2)( )
| A. | 电势能增大1.5×10-4J,动能增大 1.015×10-2J | |
| B. | 电势能减小1.5×10-4J,动能增大 0.985×10-2J | |
| C. | 电势能减小1.5×10-4J,动能增大 1.015×10-2J | |
| D. | 电势能增大1.5×10-4J,动能增大 0.985×10-2J |
2. 如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )
如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )
 如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )
如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )| A. | 如果粒子从PN边射出场区,则矩形内存在的一定是电场 | |
| B. | 如果粒子射出的速度大小不变,则矩形内存在的一定是磁场 | |
| C. | 如果粒子再回到MN上(不包括M点)时的速度大小与初速度大小相等,则矩形内存在的一定是磁场 | |
| D. | 若增加粒子的速度大小,发现粒子射出场区的时间变长,则矩形内存在的一定是磁场 |
19. 机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )
机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )
①1s
②3s
③5s
④7s.
 机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )
机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )①1s
②3s
③5s
④7s.
| A. | 只有①对 | B. | 只有②对 | C. | 只有①②对 | D. | ①②③④都对 |
 如图所示,长为L的轻杆下端用铰链固定在光滑的水平面上的C点,上端有一个质量为m的光滑小球A(视为质点),小球旁轻靠有一正方体滑块B.若用一大小为mg的水平恒力(g为重力加速度大小)向右作用于小球A,当杆与水平面成θ=30°角时A、B恰好分离,求:(提示:在圆周运动过程中任一点,质点所受的向心力与其速率的关系为F向=m$\frac{{v}^{2}}{L}$)
如图所示,长为L的轻杆下端用铰链固定在光滑的水平面上的C点,上端有一个质量为m的光滑小球A(视为质点),小球旁轻靠有一正方体滑块B.若用一大小为mg的水平恒力(g为重力加速度大小)向右作用于小球A,当杆与水平面成θ=30°角时A、B恰好分离,求:(提示:在圆周运动过程中任一点,质点所受的向心力与其速率的关系为F向=m$\frac{{v}^{2}}{L}$) 一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的极靠近A点处以60°的入射角入射,求:该光线从射入透明体到第一次射出透明体时,共经历的时间(已知真空中的光速为c;计算结果用R、n、c表示).
一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的极靠近A点处以60°的入射角入射,求:该光线从射入透明体到第一次射出透明体时,共经历的时间(已知真空中的光速为c;计算结果用R、n、c表示).
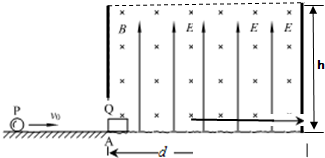
 如图所示的xoy坐标系中,x轴上方,y轴与MN之间区域内有沿x轴正向的匀强电场,场强的大小E1=1.5×105N/C;x轴上方,MN右侧足够大的区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B=0.2T.在原点O处有一粒子源,沿纸面向电场中各方向均匀地射出速率均为v0=1.0×106m/s的某种带正电粒子,粒子质量m=6.4×10-27kg,电荷量q=3.2×10-19C,粒子可以无阻碍地通过边界MN进入磁场.已知ON=0.2m.不计粒子的重力,图中MN与y轴平行.求:
如图所示的xoy坐标系中,x轴上方,y轴与MN之间区域内有沿x轴正向的匀强电场,场强的大小E1=1.5×105N/C;x轴上方,MN右侧足够大的区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B=0.2T.在原点O处有一粒子源,沿纸面向电场中各方向均匀地射出速率均为v0=1.0×106m/s的某种带正电粒子,粒子质量m=6.4×10-27kg,电荷量q=3.2×10-19C,粒子可以无阻碍地通过边界MN进入磁场.已知ON=0.2m.不计粒子的重力,图中MN与y轴平行.求: