题目内容
18. 一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的极靠近A点处以60°的入射角入射,求:该光线从射入透明体到第一次射出透明体时,共经历的时间(已知真空中的光速为c;计算结果用R、n、c表示).
一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的极靠近A点处以60°的入射角入射,求:该光线从射入透明体到第一次射出透明体时,共经历的时间(已知真空中的光速为c;计算结果用R、n、c表示).
分析 由sinC=$\frac{1}{n}$求出临界角C.已知入射角为i=60°,由折射定律求出光线从射入透明体的折射角r,判断光线在圆弧上能否发生全反射,作出光路图,由几何知识求解光线在透明体内的路程s,光线在透明体的速度为v=$\frac{c}{n}$,通过的时间为t=$\frac{s}{v}$.
解答 解: (2)由折射定律得:
(2)由折射定律得:
n=$\frac{sin60°}{sin∠1}$
得∠1=30°
由几何关系,得∠3=60°
设临界角C,sinC=$\frac{1}{n}$=$\frac{\sqrt{3}}{3}$
sinC<sin∠3,C<∠3,光线在C点发生全反射,此后光线水平反射至圆弧上的D点并在D点发生全反射,再反射至B点,从B点第一次射出.
由几何关系得,在透明体内的路光在透明体内运动路径 s=3R
光线在透明体的速度为 v=$\frac{c}{n}$
则所求时间为 t=$\frac{s}{v}$=$\frac{3nR}{c}$
答:该光线从射入透明体到第一次射出透明体时,共经历的时间为$\frac{3nR}{c}$.
点评 画出光路图是基础,判断能否发生全反射是关键.运用几何知识求出光线在透明体通过的总路程.

练习册系列答案
相关题目
8. 如图所示,图甲中M为一电动机,当滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是( )
如图所示,图甲中M为一电动机,当滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是( )
 如图所示,图甲中M为一电动机,当滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是( )
如图所示,图甲中M为一电动机,当滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是( )| A. | 电路中电源电动势为3.6V | |
| B. | 变阻器向右滑动时,V2读数逐渐减小 | |
| C. | 此过程中,电动机的输出功率最大值为0.894W | |
| D. | 变阻器的最大阻值为30Ω |
6.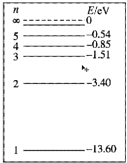 用大量具有12.5eV动能的电子,撞击大量处于基态的氢原子,观测到了一定数量的氢原子的光谱线.氢原子的能级图如图所示,下列说法中正确的是( )
用大量具有12.5eV动能的电子,撞击大量处于基态的氢原子,观测到了一定数量的氢原子的光谱线.氢原子的能级图如图所示,下列说法中正确的是( )
 用大量具有12.5eV动能的电子,撞击大量处于基态的氢原子,观测到了一定数量的氢原子的光谱线.氢原子的能级图如图所示,下列说法中正确的是( )
用大量具有12.5eV动能的电子,撞击大量处于基态的氢原子,观测到了一定数量的氢原子的光谱线.氢原子的能级图如图所示,下列说法中正确的是( )| A. | 实验中能产生三种频率的谱线 | |
| B. | 波长最长的光子具有的能量为1.89eV | |
| C. | 频率最高的光子具有的能量为12.5eV | |
| D. | 电子撞击后的动能一定为2.3eV |
13.在“测定直流电动机的效率”实验中,用图1所示的电路测定一个额定电压为6V、额定功率为3W的直流电动机的机械效率.

①根据电路图完成实物图的连线(图2);
②实验中保持电动机两端电压U恒为6V,重物每次匀速上升的高度h均为1.5m,所测物理量及测量结果如表所示:
计算电动机效率η的表达式为$η=\frac{mgh}{UIt}×100%$(用符号表示),第4次实验中电动机工作效率为74%.
③在第5次实验中,电动机的输出功率是0;可估算出电动机线圈的电阻为2.4Ω.

①根据电路图完成实物图的连线(图2);
②实验中保持电动机两端电压U恒为6V,重物每次匀速上升的高度h均为1.5m,所测物理量及测量结果如表所示:
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| 电动机的电流I/A | 0.2 | 0.4 | 0.6 | 0.8 | 2.5 |
| 所提重物的重力Mg/N | 0.8 | 2.0 | 4.0 | 6.0 | 6.5 |
| 重物上升时间t/s | 1.4 | 1.65 | 2.1 | 2.7 | 重物不运动 |
③在第5次实验中,电动机的输出功率是0;可估算出电动机线圈的电阻为2.4Ω.
3.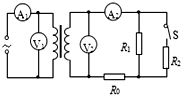 如图是通过理想变压器降压给用户供电的示意图.变压器输入电压是市区电网的电压,负载变化时输入电压不会有大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,开关S闭合后,相当于接入电路中工作的用电器增加.则关于开关S闭合后,以下说法正确的是( )
如图是通过理想变压器降压给用户供电的示意图.变压器输入电压是市区电网的电压,负载变化时输入电压不会有大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,开关S闭合后,相当于接入电路中工作的用电器增加.则关于开关S闭合后,以下说法正确的是( )
 如图是通过理想变压器降压给用户供电的示意图.变压器输入电压是市区电网的电压,负载变化时输入电压不会有大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,开关S闭合后,相当于接入电路中工作的用电器增加.则关于开关S闭合后,以下说法正确的是( )
如图是通过理想变压器降压给用户供电的示意图.变压器输入电压是市区电网的电压,负载变化时输入电压不会有大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,开关S闭合后,相当于接入电路中工作的用电器增加.则关于开关S闭合后,以下说法正确的是( )| A. | 电表V1示数不变,V2示数减小 | B. | 电表A1示数增大、A2示数增大 | ||
| C. | 原线圈输入功率减小 | D. | 电阻R1两端的电压减小 |
10.2013年12月14日21时11分,“嫦娥三号”在月球正面的虹湾以东地区着陆,假设着陆前,“嫦娥三号”探月卫星绕月球表面匀速飞行(不计周围其他天体的影响),宇航员测出“嫦娥三号”飞行N圈用时为t,已知地球质量为M,地球半径为R,月球半径为r,地球表面重力加速度为g,则( )
| A. | “嫦娥三号”探月卫星匀速飞行的速度为$\frac{2πNR}{t}$ | |
| B. | 月球的平均密度为$\frac{3πM{N}^{2}}{g{r}^{2}{t}^{2}}$ | |
| C. | “嫦娥三号”探月卫星的质量为$\frac{4{π}^{2}{N}^{2}{r}^{3}}{g{R}^{2}{t}^{2}}$ | |
| D. | “嫦娥三号”探月卫星绕月球表面匀速飞行的向心加速度为$\frac{4{π}^{2}{N}^{2}r}{{t}^{2}}$ |
7.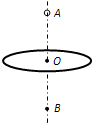 如图所示,一固定的水平玻璃圆环均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.现将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度υ0,重力加速度为g,则下列判断正确的是( )
如图所示,一固定的水平玻璃圆环均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.现将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度υ0,重力加速度为g,则下列判断正确的是( )
 如图所示,一固定的水平玻璃圆环均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.现将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度υ0,重力加速度为g,则下列判断正确的是( )
如图所示,一固定的水平玻璃圆环均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.现将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度υ0,重力加速度为g,则下列判断正确的是( )| A. | 带电圆环在B点产生的场强方向竖直向上 | |
| B. | 小球从A点运动到B点的过程中电场力一直做负功 | |
| C. | 小球从A点运动到B点的过程中通过O点时速度最大 | |
| D. | 小球通过B点时的速度为$\sqrt{{{v}_{0}}^{2}+4gh}$ |
8. 如图所示,质量为M倾角为θ=30°的斜面体放在水平地面上,质量为m的物体A放在的斜面上时,恰好能匀速下滑.现用细线系住物体A,并平行于斜面向上绕过光滑的定滑轮,另一端系住质量也为m的物体B,让物体B以一定的初速度向下运动,在物体A、B运动过程中斜面体保持静止不动,下列叙述中正确的是( )
如图所示,质量为M倾角为θ=30°的斜面体放在水平地面上,质量为m的物体A放在的斜面上时,恰好能匀速下滑.现用细线系住物体A,并平行于斜面向上绕过光滑的定滑轮,另一端系住质量也为m的物体B,让物体B以一定的初速度向下运动,在物体A、B运动过程中斜面体保持静止不动,下列叙述中正确的是( )
 如图所示,质量为M倾角为θ=30°的斜面体放在水平地面上,质量为m的物体A放在的斜面上时,恰好能匀速下滑.现用细线系住物体A,并平行于斜面向上绕过光滑的定滑轮,另一端系住质量也为m的物体B,让物体B以一定的初速度向下运动,在物体A、B运动过程中斜面体保持静止不动,下列叙述中正确的是( )
如图所示,质量为M倾角为θ=30°的斜面体放在水平地面上,质量为m的物体A放在的斜面上时,恰好能匀速下滑.现用细线系住物体A,并平行于斜面向上绕过光滑的定滑轮,另一端系住质量也为m的物体B,让物体B以一定的初速度向下运动,在物体A、B运动过程中斜面体保持静止不动,下列叙述中正确的是( )| A. | 物体A加速向上运动 | B. | 物体B处于超重状态 | ||
| C. | 地面对斜面体没有摩擦力作用 | D. | 地面对斜面体的摩擦力向左 |
