题目内容
13. 如图所示,垂直纸面向里的匀强磁场的宽度为h1,矩形线圈abcd的质量为m=0.016kg,电阻R=0.1Ω,ab边的长度为l=0.5m.bc边的长度为d=0.1m,矩形线圈cd边到磁场的上边界的距离为h2=5m,矩形线圈从该位置由静止开始自由下落,线圈cd边刚进入磁场时恰好做匀速运动,线圈在下落过程中始终保持竖直,不计空气阻力,g=10m/s2,求:
如图所示,垂直纸面向里的匀强磁场的宽度为h1,矩形线圈abcd的质量为m=0.016kg,电阻R=0.1Ω,ab边的长度为l=0.5m.bc边的长度为d=0.1m,矩形线圈cd边到磁场的上边界的距离为h2=5m,矩形线圈从该位置由静止开始自由下落,线圈cd边刚进入磁场时恰好做匀速运动,线圈在下落过程中始终保持竖直,不计空气阻力,g=10m/s2,求:(1)该磁场的磁感应强度B的大小;
(2)若矩形线圈cd边通过磁场经历的时间为0.15s,则磁场的宽度h1为多大.
分析 (1)由机械能守恒定律求出线圈进入磁场时的速度,然后由平衡条件和安培力与速度的关系式,求出磁感应强度B.
(2)先求出线框匀速进入磁场的时间,然后求出线框做匀加速运动的时间,再求出磁场的宽度h2.
解答 解:(1)线圈在磁场外做自由落体运动时,其机械能守恒,由机械能守恒定律得:
mgh2=$\frac{1}{2}$mv02
得 v0=$\sqrt{2g{h}_{2}}$=$\sqrt{2×10×5}$=10m/s
线圈进入磁场时受到的安培力:F=BIl=B$\frac{Bl{v}_{0}}{R}$l=$\frac{{B}^{2}{l}^{2}{v}_{0}}{R}$
线圈进入磁场时做匀速直线运动,由平衡条件得:mg=F
联立代入数据解得:B=0.08T;
(2)线圈下边dc进入磁场后先做匀速运动,做匀速直线运动的时间:t1=$\frac{d}{{v}_{0}}$=$\frac{0.1}{10}$=0.01s
线圈完全在磁场中做匀加速运动的时间为:t2=t-t1=0.15s-0.01s=0.14s
磁场的宽度h1为:h1=d+(v0t1+$\frac{1}{2}$gt12)=0.1+(10×0.14+$\frac{1}{2}$×10×0.142)=1.598m;
答:
(1)该磁场的磁感应强度B的大小是0.08T;
(2)若矩形线圈cd边通过磁场经历的时间为0.15s,则磁场的宽度h1为1.598m.
点评 本题电磁感应中力学问题,分析物体的受力情况和运动情况是基础,还要能熟练推导出安培力与速度的关系式.

练习册系列答案
相关题目
8. 某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:
某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:
(A)表面光滑的长木板(长度为L),
(B)小车,
(C)质量为m的钩码若干个,
(D)方木块(备用于垫木板),
(E)米尺,
(F)秒表.
(1)实验过程:
第一步,在保持斜面倾角不变时,探究加速度与质量的关系.
实验中,通过向小车放入钩码来改变物体质量,只要测出小车由斜面顶端滑至底端所用时间t,就可以由公式a=$\frac{2L}{{t}^{2}}$求出a.某同学记录了数据如表所示:
根据以上信息,我们发现,在实验误差范围内质量改变之后平均下滑时间不改变(填“改变”或“不改变”),经过分析得出加速度与质量的关系为斜面倾角一定时,加速度与物体质量无.
第二步,在物体质量不变时,探究加速度与倾角的关系.实验中通过改变方木块垫放位置来调整长木板的倾角,由于没有量角器,因此通过测量出木板顶端到水平面高度h,求出倾角α的正弦值sinα=$\frac{h}{L}$.某同学记录了高度和加速度的对应值,并在坐标纸上建立适当的坐标轴后描点作图如图,请根据他所作的图线求出当地的重力加速度g=10m/s2.进一步分析可知,光滑斜面上物体下滑的加速度与倾角的关系为a=gsinα.
 某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:
某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:(A)表面光滑的长木板(长度为L),
(B)小车,
(C)质量为m的钩码若干个,
(D)方木块(备用于垫木板),
(E)米尺,
(F)秒表.
(1)实验过程:
第一步,在保持斜面倾角不变时,探究加速度与质量的关系.
实验中,通过向小车放入钩码来改变物体质量,只要测出小车由斜面顶端滑至底端所用时间t,就可以由公式a=$\frac{2L}{{t}^{2}}$求出a.某同学记录了数据如表所示:
 | M | M+m | M+2m |
| 1 | 1.42 | 1.41 | 1.42 |
| 2 | 1.40 | 1.42 | 1.39 |
| 3 | 1.41 | 1.38 | 1.42 |
第二步,在物体质量不变时,探究加速度与倾角的关系.实验中通过改变方木块垫放位置来调整长木板的倾角,由于没有量角器,因此通过测量出木板顶端到水平面高度h,求出倾角α的正弦值sinα=$\frac{h}{L}$.某同学记录了高度和加速度的对应值,并在坐标纸上建立适当的坐标轴后描点作图如图,请根据他所作的图线求出当地的重力加速度g=10m/s2.进一步分析可知,光滑斜面上物体下滑的加速度与倾角的关系为a=gsinα.
5.一电子飞经电场中A、B两点,电子在A点的电势能4.8×10-17J,动能为3.2×10-17J,电子经过B点的电势能为3.2×10-17J,如果电子只受电场力作用,则( )
| A. | 电子在B点的动能为4.8×10-17J | B. | 由A点到B点电场力做功为100eV | ||
| C. | 电子在B点的动能为1.6×10-17J | D. | A、B两点间电势差为100V |
2. 在如图所示的虚线框内有匀强磁场,磁感应强度随时间均匀变化,半径为r、匝数为n的圆形线圈有一半处在磁场中,磁场方向垂直于线圈平面,此时线圈的发热功率恒为P.下列说法正确的是( )
在如图所示的虚线框内有匀强磁场,磁感应强度随时间均匀变化,半径为r、匝数为n的圆形线圈有一半处在磁场中,磁场方向垂直于线圈平面,此时线圈的发热功率恒为P.下列说法正确的是( )
 在如图所示的虚线框内有匀强磁场,磁感应强度随时间均匀变化,半径为r、匝数为n的圆形线圈有一半处在磁场中,磁场方向垂直于线圈平面,此时线圈的发热功率恒为P.下列说法正确的是( )
在如图所示的虚线框内有匀强磁场,磁感应强度随时间均匀变化,半径为r、匝数为n的圆形线圈有一半处在磁场中,磁场方向垂直于线圈平面,此时线圈的发热功率恒为P.下列说法正确的是( )| A. | 若只将线圈全部置于磁场中,则线圈的发热功率变为2P | |
| B. | 若只将线圈全部置于磁场中,则线圈的发热功率仍为P | |
| C. | 若只将线圈的半径增大到原来的2倍,仍保持线圈有一半面积在磁场中,则线圈的发热功率变为2P | |
| D. | 若只将线圈的匝数增大到原来的2倍,则线圈的发热功率变为2P |
3.量子通讯卫星是一种传输高效的通信卫星,彻底杜绝间谍窃听及破解的保密通信技术,具有很强的抗衡外国的网络攻击与防御能力,2016年8月16日,我国首颗量子卫星(“墨子号”)成功升空,运行在高度约500km的圆形轨道上,下列说法正确的是( )
| A. | 量子卫星的轨道平面可能与北京同纬度的轨道平面重合 | |
| B. | 量子卫星运行的周期比同步卫星的运行周期大 | |
| C. | 量子卫星运行的线速度比同步卫星运行的线速度小 | |
| D. | 量子卫星运行的向心加速度比同步卫星运行的向心加速度大 |
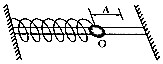 一质点作简谐振动,它离开平衡的位移s(厘米)与时间t(秒)的关系为s=10sin(6πt+$\frac{π}{6}$).
一质点作简谐振动,它离开平衡的位移s(厘米)与时间t(秒)的关系为s=10sin(6πt+$\frac{π}{6}$).

