题目内容
1.某同学做了“用单摆测定重力加速度”的实验.
(1)测摆长时测量结果如图1所示(单摆的另一端与刻度尺的零刻线对齐),则摆长为99.85cm.然后用秒表记录了单摆做50次全振动所用的时间如图2所示,则秒表读数为100.6s.
(2)根据该同学的测量结果,若取π2=9.86,则其所测量的重力加速度值为9.73m/s2.(取三位有效数字)
(3)如果该同学测得的g值偏小,可能的原因是BC
A.测摆长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现了松动,使摆线长度增加了
C.开始计时时,秒表开始计时按钮提前按下,但终止计时按钮准时按下
D.实验中误将49次的全振动数成了50次全振动.
分析 (1)摆长等于摆线的长度与摆球的半径之间,即悬点到球心的距离.秒表的读数等于小盘读数加上大盘读数.
(2)根据单摆全振动的次数求出单摆的周期,结合单摆的周期公式求出重力加速度.
(3)根据单摆的周期公式得出重力加速度的表达式,结合周期和摆长的测量误差分析重力加速度的测量误差.
解答 解:(1)刻度尺的读数需读到最小刻度的下一位,摆长等于悬点到球心的距离,则摆长为99.85cm.
秒表的小盘读数为90s,大盘读数为10.6s,则最终读数为100.6s.
(2)单摆的周期T=$\frac{100.6}{50}s$=2.012s,根据T=$2π\sqrt{\frac{l}{g}}$得,g=$\frac{4{π}^{2}l}{{T}^{2}}=\frac{4×9.86×0.9985}{2.01{2}^{2}}=9.73m/{s}^{2}$.
(3)根据T=$2π\sqrt{\frac{l}{g}}$得,g=$\frac{4{π}^{2}l}{{T}^{2}}$,
A、测摆线长时摆线拉得过紧,l测量值偏大,则g测量值偏大,故A错误;
B、摆线上端未牢固地系于悬点,振动中出现了松动,使摆线长度增加了,测量值l偏小,g测量值偏小,故B正确;
C、开始计时时,秒表提前按下,周期测量值偏大,则g测量值偏小,故C正确;
D、n增大,则周期测量值偏小,g测量值增大,故D错误;
故选BC.
故答案为:(1)99.85,100.6;
(2)9.73;
(3)BC.
点评 解决本题的关键掌握刻度尺、秒表的读数方法,掌握单摆的周期公式,会根据周期、摆长的测量误差分析重力加速度的测量误差,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列说法正确的是( )
| A. | 光子像其他粒子一样,不但具有能量,也具有动量 | |
| B. | 原子核结合能越大,原子核越稳定 | |
| C. | 核泄漏事故污染物CS137能够产生对人体有害的辐射,其核反应方程式为${\;}_{55}^{137}$CS→${\;}_{56}^{137}$Ba+x可以判断x为电子 | |
| D. | β射线在云室中穿过会留下清晰的直线径迹,说明β射线也有波动性 | |
| E. | 一个氢原子处在n=4的能级,当它跃迁到较低能级时,最多可发出3种频率的光子 |
9. 如图所示,在半径为R的圆形区域内有匀强磁场,在边长为2R的正方形区域里也有匀强磁场.两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )
如图所示,在半径为R的圆形区域内有匀强磁场,在边长为2R的正方形区域里也有匀强磁场.两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )
 如图所示,在半径为R的圆形区域内有匀强磁场,在边长为2R的正方形区域里也有匀强磁场.两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )
如图所示,在半径为R的圆形区域内有匀强磁场,在边长为2R的正方形区域里也有匀强磁场.两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )| A. | 带电粒子在磁场中飞行的时间一定不同 | |
| B. | 从M点射入的带电粒子可能先飞出磁场 | |
| C. | 从N点射入的带电粒子可能先飞出磁场 | |
| D. | 从N点射入的带电粒子不可能比M点射入的带电粒子先飞出磁场 |
16.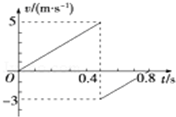 质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )
质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )
 质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )
质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )| A. | 小球第一次反弹后离开地面的速度的大小为5m/s | |
| B. | 碰撞前后动量改变量的大小为8kg•m/s | |
| C. | 小球是从1.25m高处自由下落的 | |
| D. | 小球反弹起的最大高度为0.45 m |
13.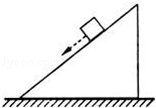 如图所示,质量为M的斜面体放在水平面上,斜面上放一质量为m的物块,当给物块一沿斜面向下的初速度v0时,物块可在斜面上匀速下滑;若在给物块沿斜面向下初速度v0的同时,在物块上施加一平行于斜面向下的拉力,物块可沿斜面加速运动.已知两种情况下斜面体都处于静止状态,则后一种情况和前一种情况相比( )
如图所示,质量为M的斜面体放在水平面上,斜面上放一质量为m的物块,当给物块一沿斜面向下的初速度v0时,物块可在斜面上匀速下滑;若在给物块沿斜面向下初速度v0的同时,在物块上施加一平行于斜面向下的拉力,物块可沿斜面加速运动.已知两种情况下斜面体都处于静止状态,则后一种情况和前一种情况相比( )
 如图所示,质量为M的斜面体放在水平面上,斜面上放一质量为m的物块,当给物块一沿斜面向下的初速度v0时,物块可在斜面上匀速下滑;若在给物块沿斜面向下初速度v0的同时,在物块上施加一平行于斜面向下的拉力,物块可沿斜面加速运动.已知两种情况下斜面体都处于静止状态,则后一种情况和前一种情况相比( )
如图所示,质量为M的斜面体放在水平面上,斜面上放一质量为m的物块,当给物块一沿斜面向下的初速度v0时,物块可在斜面上匀速下滑;若在给物块沿斜面向下初速度v0的同时,在物块上施加一平行于斜面向下的拉力,物块可沿斜面加速运动.已知两种情况下斜面体都处于静止状态,则后一种情况和前一种情况相比( )| A. | 物块对斜面体的压力变大 | B. | 斜面体受地面的摩擦力不变 | ||
| C. | 斜面体对地面的压力变大 | D. | 斜面体受地面的摩擦力变小 |
10.小船在180m宽的河中横渡,水流速度是4m/s,船在静水中的航速是5m/s,则下列判断正确的是( )
| A. | 小船过河所需的最短时间是36s | |
| B. | 要使小船过河的位移最短,船头应始终正对着对岸 | |
| C. | 要使小船过河的位移最短,过河所需的时间是60s | |
| D. | 如果水流速度增大为6m/s,小船过河所需的最短时间将不变 |

 如图所示,小球从倾斜轨道上静止释放,下滑到水平轨道,当小球通过水平轨道末端的瞬间,前方的圆筒立即开始匀速转动,圆筒下方有一小孔P,圆筒静止时小孔正对着轨道方向.已知圆筒顶端与水平轨道在同一水平面,水平轨道末端与圆筒顶端圆心的距离为d,P孔距圆筒顶端的高度差为h,圆筒半径为R,现观察到小球从轨道滑下后,恰好钻进P孔,小球可视为质点.求:
如图所示,小球从倾斜轨道上静止释放,下滑到水平轨道,当小球通过水平轨道末端的瞬间,前方的圆筒立即开始匀速转动,圆筒下方有一小孔P,圆筒静止时小孔正对着轨道方向.已知圆筒顶端与水平轨道在同一水平面,水平轨道末端与圆筒顶端圆心的距离为d,P孔距圆筒顶端的高度差为h,圆筒半径为R,现观察到小球从轨道滑下后,恰好钻进P孔,小球可视为质点.求: 在做“研究平抛运动”的实验时,让小球多次沿同一斜槽轨道滑下,通过描点法画小球做平抛运动的轨迹.为了能较准确地描绘运动轨迹,下面列出了一些操作要求,将你认为正确的选项前面的字母填在横线上ab.
在做“研究平抛运动”的实验时,让小球多次沿同一斜槽轨道滑下,通过描点法画小球做平抛运动的轨迹.为了能较准确地描绘运动轨迹,下面列出了一些操作要求,将你认为正确的选项前面的字母填在横线上ab.