题目内容
2. 如图所示,轻质弹簧的自然长度为L0,劲度系数为k,现用水平推力缓慢地推弹簧,使弹簧缩短△x,求推力做的功,以及弹簧弹性势能的增加量.
如图所示,轻质弹簧的自然长度为L0,劲度系数为k,现用水平推力缓慢地推弹簧,使弹簧缩短△x,求推力做的功,以及弹簧弹性势能的增加量.
分析 根据胡克定律找到力与位移关系,用推力的平均值求推力做功,再由功能原理求弹簧弹性势能的增加量.
解答 解:根据平衡条件和胡克定律得
推力 F=kx,x是弹簧压缩的长度,可知F与x成正比,则推力做的功为 W=$\overline{F}$△x=$\frac{0+k△x}{2}△x$=$\frac{1}{2}k△{x}^{2}$
根据功能原理可知,弹簧弹性势能的增加量△Ep=W=$\frac{1}{2}k△{x}^{2}$
答:推力做的功是$\frac{1}{2}k△{x}^{2}$,弹簧弹性势能的增加量是$\frac{1}{2}k△{x}^{2}$.
点评 本题中推力是变力,要用力的平均值求功,由于力随位移均匀增大,才能用本题的方法求功,也可以作出F与x的图象,由面积求功.

练习册系列答案
相关题目
12. 如图所示,水平面上两根平行导轨的左端a、b接有电阻R,匀强磁场方向竖直向下,由于导体棒cd在导轨上运动,电阻R上产生从a到b并且逐渐变大的电流,下列说法正确的是( )
如图所示,水平面上两根平行导轨的左端a、b接有电阻R,匀强磁场方向竖直向下,由于导体棒cd在导轨上运动,电阻R上产生从a到b并且逐渐变大的电流,下列说法正确的是( )
 如图所示,水平面上两根平行导轨的左端a、b接有电阻R,匀强磁场方向竖直向下,由于导体棒cd在导轨上运动,电阻R上产生从a到b并且逐渐变大的电流,下列说法正确的是( )
如图所示,水平面上两根平行导轨的左端a、b接有电阻R,匀强磁场方向竖直向下,由于导体棒cd在导轨上运动,电阻R上产生从a到b并且逐渐变大的电流,下列说法正确的是( )| A. | 导体棒cd向左减速运动 | B. | 导体棒cd向左加速运动 | ||
| C. | 导体棒cd向右减速运动 | D. | 导体棒cd向右加速运动 |
10.区分横波和纵波的依据是( )
| A. | 质点沿水平方向还是沿竖直方向振动 | |
| B. | 波沿水平方向还是沿竖直方向传播 | |
| C. | 质点的振动方向和波的传播方向是相互垂直还是平行 | |
| D. | 波传播距离的远近 |

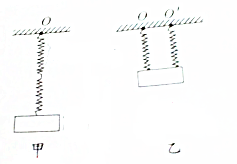 如图甲所示,用两根完全相同的弹簧连接起来悬挂一质量m=1kg的物体.若弹簧的原长l0=20 cm,劲度系数k=100 N/m,不计弹簧的质量.(取g=10 N/kg)
如图甲所示,用两根完全相同的弹簧连接起来悬挂一质量m=1kg的物体.若弹簧的原长l0=20 cm,劲度系数k=100 N/m,不计弹簧的质量.(取g=10 N/kg) 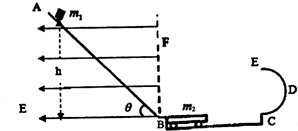 安庆市某中学物理兴趣小组设计了如图所示的轨道,AB为动摩擦因素μ1=0.25的倾斜轨道,斜面倾角θ=53°,竖直边界BF的左侧空间存在场强大小E=5×104V/m,方向水平向左的匀强磁场.底端有一小段将其转接为水平的弧形轨道(m1从斜面过渡到小车上时不考虑动能的损失),BC是一个光滑的水平凹槽,凹槽内放置一个质量为m2=$\frac{1}{3}$kg的小车,小车上表面与凹槽的两端点BC等高,CDE是光滑的半径为R=0.2m的竖直半圆形轨道,E是圆轨道的最高点.将一个质量为m1=1kg、带正电q=1.5×10-4C的小滑块(可视为质点),以初速度v0=3m/s从AB轨道上离B点高h=5.6m处开始释放,滑块下滑后从B点滑上小车,在到达C点之前,滑块与小车达到共同速度,小车与凹槽碰撞后立即停止,此后滑块继续运动,小车的长度L=1.5m.滑块与小车之间的动摩擦因数μ2=0.2,g=10m/s2.试求:
安庆市某中学物理兴趣小组设计了如图所示的轨道,AB为动摩擦因素μ1=0.25的倾斜轨道,斜面倾角θ=53°,竖直边界BF的左侧空间存在场强大小E=5×104V/m,方向水平向左的匀强磁场.底端有一小段将其转接为水平的弧形轨道(m1从斜面过渡到小车上时不考虑动能的损失),BC是一个光滑的水平凹槽,凹槽内放置一个质量为m2=$\frac{1}{3}$kg的小车,小车上表面与凹槽的两端点BC等高,CDE是光滑的半径为R=0.2m的竖直半圆形轨道,E是圆轨道的最高点.将一个质量为m1=1kg、带正电q=1.5×10-4C的小滑块(可视为质点),以初速度v0=3m/s从AB轨道上离B点高h=5.6m处开始释放,滑块下滑后从B点滑上小车,在到达C点之前,滑块与小车达到共同速度,小车与凹槽碰撞后立即停止,此后滑块继续运动,小车的长度L=1.5m.滑块与小车之间的动摩擦因数μ2=0.2,g=10m/s2.试求: 民用航空客机的机舱一般都设有紧急出口,飞机发生意外情况着陆后,打开紧急出口的舱门,会自动生成一个气囊(由斜面AC部分和水平面CD部分构成的).如图所示为某气囊斜面,机舱离底端的竖直高度AB=3.0m,斜面长AC=5.0m,斜面与水平面CD段间有一段小圆弧平滑连接,一个质量m=60kg的旅客从气囊上由静止开始滑下,最后滑到水平面上的某点静止,已知旅客与气囊斜面部分及水平面部分的动摩擦因数均为μ=0.5.(不计空气阻力,计算结果可保留根号).求:
民用航空客机的机舱一般都设有紧急出口,飞机发生意外情况着陆后,打开紧急出口的舱门,会自动生成一个气囊(由斜面AC部分和水平面CD部分构成的).如图所示为某气囊斜面,机舱离底端的竖直高度AB=3.0m,斜面长AC=5.0m,斜面与水平面CD段间有一段小圆弧平滑连接,一个质量m=60kg的旅客从气囊上由静止开始滑下,最后滑到水平面上的某点静止,已知旅客与气囊斜面部分及水平面部分的动摩擦因数均为μ=0.5.(不计空气阻力,计算结果可保留根号).求: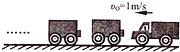 某辆货车以v0=1m/s的速度驶向停在水平道路上的9节挂车,与它们对接,设货车和挂车的质量都相等,水平道路的摩擦忽略不计.货车与笫一节挂车相碰后,它们连在一起具有一个相同的速度是0.5m/s;紧接着又与第二节挂车相碰,就这样直至碰上最后一节挂车,与最后一节碰撞后,整体的速度0.1m/s.
某辆货车以v0=1m/s的速度驶向停在水平道路上的9节挂车,与它们对接,设货车和挂车的质量都相等,水平道路的摩擦忽略不计.货车与笫一节挂车相碰后,它们连在一起具有一个相同的速度是0.5m/s;紧接着又与第二节挂车相碰,就这样直至碰上最后一节挂车,与最后一节碰撞后,整体的速度0.1m/s.