题目内容
13.如图甲所示,一个带负电荷的液滴静止在一个平行板电容器中靠近下板的M点,电容器的电压为U0.现将t=0时电容器的电压变为2U0,t=t0时刻电压突变为零,然后电压在零和2U0之间交替变化,如图乙所示.使带电液滴在M与N之间做往复运动,设带电液滴未碰到极板,求:
(1)电压变化的周期.
(2)平行板电容器内场强的最大值.
分析 (1)根据平衡求出电场力和液滴所受重力的关系,当电压变化后,根据牛顿第二定律求出加速度,以及撤去电压后的加速度,分析出液滴的运动规律,根据运动学公式求出周期的大小.
(2)根据液滴的运动规律得出两极板距离的最小值,根据电势差和电场强度的关系求出电场强度的最大值.
解答 解:(1)液滴开始处于静止,根据平衡有:$\frac{q{U}_{0}}{d}=mg$,
当电压为2U0时,根据牛顿第二定律得,a=$\frac{\frac{q•2{U}_{0}}{d}-mg}{m}$=g,
t0时刻,速度v=at0=gt0,
撤去电压,液滴做竖直上抛运动,液滴速度减为零的时间$t′=\frac{v}{g}={t}_{0}$,
然后再经过t0,恢复电压2U0,再经过t0液滴返回出发点,以后重复之前的运动,可知电压变化的周期T=4t0.
(2)电场强度E=$\frac{2{U}_{0}}{d}$,当d最小时,电场强度为最大值,
${d}_{min}=2×\frac{1}{2}g{{t}_{0}}^{2}=g{{t}_{0}}^{2}$,
则电场强度的最大值${E}_{max}=\frac{2{U}_{0}}{g{{t}_{0}}^{2}}$.
答:(1)电压的变化周期为4t0;
(2)平行板电容器内场强的最大值为$\frac{2{U}_{0}}{g{{t}_{0}}^{2}}$.
点评 解决本题的关键理清液滴在整个过程中的运动规律,通过液滴运动的周期性得出电源变化的周期,知道当两极板间的距离最小时,电场强度最大,通过运动学公式求出最小距离是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
 如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )| A. | 物体开始运动后加速度大小可以大于g | |
| B. | 物体开始运动后加速度不断减小 | |
| C. | 经过时间t=$\frac{mg}{μkq}$,物体在竖直墙壁上的位移达到最大值 | |
| D. | 经过时间t=$\frac{mg}{μkq}$,物体运动速度达最大值 |
3. 如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )
如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )
 如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )
如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )| A. | vC=3 m/s | B. | vB=$\sqrt{8}$ m/s | ||
| C. | DE=3 m | D. | 从D到E所用时间为4 s |
 如图所示,正点电荷其中的一条电场线与x轴重合,一带正电的粒子从x轴上的a点由静止开始仅在电场力作用下运动到b点.在此运动过程中,下列关于粒子运动速度v随时间t的变化,电场强度E和运动径迹上电势φ、粒子的电势能EP随位移x的变化图象可能正确的是( )
如图所示,正点电荷其中的一条电场线与x轴重合,一带正电的粒子从x轴上的a点由静止开始仅在电场力作用下运动到b点.在此运动过程中,下列关于粒子运动速度v随时间t的变化,电场强度E和运动径迹上电势φ、粒子的电势能EP随位移x的变化图象可能正确的是( )



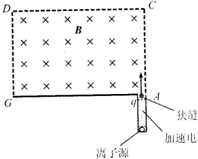 利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.
利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用. 如图所示为一组未知方向的匀强电场的电场线,将1×10-6C的负电荷由A点沿水平线移至B点,静电力做了2×10-6J的功,A,B间的距离为2cm.匀强电场场强大小200V/m;方向斜向上方.
如图所示为一组未知方向的匀强电场的电场线,将1×10-6C的负电荷由A点沿水平线移至B点,静电力做了2×10-6J的功,A,B间的距离为2cm.匀强电场场强大小200V/m;方向斜向上方.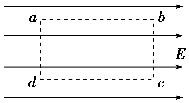 如图所示的匀强电场场强为103 N/C,沿电场线方向ab=dc=4cm垂直电场线方向bc=ad=3cm.则ab之间的电势差为40V,若将q=-5×10-3 C的点电荷沿矩形路径abcd移动一周,电场力做功是0J.
如图所示的匀强电场场强为103 N/C,沿电场线方向ab=dc=4cm垂直电场线方向bc=ad=3cm.则ab之间的电势差为40V,若将q=-5×10-3 C的点电荷沿矩形路径abcd移动一周,电场力做功是0J. 如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速率、质量为m的电子.若极板长为L,间距为d.当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离A板垂直距离为$\frac{3}{4}$d.以已知电子的电荷量为e,L=2d,不计电子重力与它们之间的相互作用力.
如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速率、质量为m的电子.若极板长为L,间距为d.当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离A板垂直距离为$\frac{3}{4}$d.以已知电子的电荷量为e,L=2d,不计电子重力与它们之间的相互作用力.