题目内容
13.“嫦娥一号”是我国首次发射的探月卫星,它在距月球表面高度为h=200km的圆形轨道上运行,运行周期为T=127分钟.已知引力常量G=6.67×10-11N•m2/kg2,月球半径约为R=1.74×103km.利用以上条件写出月球密度的表达式且计算出其数值约是多少?(结果保留两位有效数字) (已知半径为R的球体体积公式V=$\frac{4}{3}$πR3)分析 嫦娥一号绕月球做圆周运动,万有引力提供向心力,已知轨道半径和运动行周期求月球质量,再根据$ρ=\frac{M}{V}$求解密度.
解答 解:根据有引力提供嫦娥一号圆周运动的向心力有:
$\frac{GMm}{{r}^{2}}=\frac{m•4{π}^{2}r}{{T}^{2}}$
得中心天体月球的质量M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$
代入轨道半径r=R+h=1.74×103+200km=1.94×106m,周期T=127min=127×60s=7620s,引力常量G=6.67×10-11N•m2/kg2
可得月球质量M=7.4×1022kg
则密度$ρ=\frac{M}{V}$=$\frac{3{π}^{\;}(R+h)}{G{T}^{2}{R}^{3}}$
代入数据得:ρ=$\frac{7.4×1{0}^{22}}{\frac{4}{3}π•(1.74×1{0}^{6})^{3}}$=3.5×103kg/m3
答:月球密度的表达式为$ρ=\frac{3{π}^{\;}(R+h)}{G{T}^{2}{R}^{3}}$,其值为3.5×103kg/m3
点评 注意万有引力提供圆周运动的向心力只能计算中心天体的质量,不能计算环绕天体的质量.

练习册系列答案
相关题目
3. 如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
 如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )| A. | 滑块克服摩擦力所做的功为fL | |
| B. | 上述过程满足(F-f)(L+s)=$\frac{1}{2}$mv12+$\frac{1}{2}{m}_{1}{{v}_{2}}^{2}$ | |
| C. | 其他条件不变的情况下,F越大,滑块到达右端所用时间越长 | |
| D. | 其他条件不变的情况下,f越大,滑块与木板间产生的热量越多 |
4. “修正带”是深受同学们欢迎的一种学习用品,某种”修正带”内部结构如图所示,经测量两个齿轮的半径分别为2.0cm和0.8cm,其中a点和c点分别位于大小齿轮边缘,b点位于大齿轮某半径的中点,当齿轮匀速转动时( )
“修正带”是深受同学们欢迎的一种学习用品,某种”修正带”内部结构如图所示,经测量两个齿轮的半径分别为2.0cm和0.8cm,其中a点和c点分别位于大小齿轮边缘,b点位于大齿轮某半径的中点,当齿轮匀速转动时( )
 “修正带”是深受同学们欢迎的一种学习用品,某种”修正带”内部结构如图所示,经测量两个齿轮的半径分别为2.0cm和0.8cm,其中a点和c点分别位于大小齿轮边缘,b点位于大齿轮某半径的中点,当齿轮匀速转动时( )
“修正带”是深受同学们欢迎的一种学习用品,某种”修正带”内部结构如图所示,经测量两个齿轮的半径分别为2.0cm和0.8cm,其中a点和c点分别位于大小齿轮边缘,b点位于大齿轮某半径的中点,当齿轮匀速转动时( )| A. | 大齿轮上的a点与大齿轮上b点的周期之比为2:5 | |
| B. | 大齿轮上的a点与小齿轮上c点角速度之比为5:2 | |
| C. | 大齿轮上的b点与小齿轮上c点线速度之比为1:1 | |
| D. | 大齿轮上的b点与小齿轮上c点角速度之比为2:5 |
1.对于曲线运动,下列说法中正确的是( )
| A. | 速度方向可能不变 | B. | 加速度一定是变化 | ||
| C. | 速度方向和加速度方向不可能一致 | D. | 合外力一定与速度方向垂直 |
8.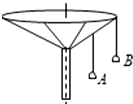 如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
 如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )| A. | A与B的角速度大小相等 | |
| B. | A与B的向心加速度大小相等 | |
| C. | 悬挂A的缆绳所受的拉力比悬挂B的小 | |
| D. | 悬挂A、B的缆绳与竖直方向的夹角相等 |
18.质量为1kg的物体从离地面5m高处自由下落.与地面碰撞后静止,设球与地面作用时间为0.2s,则小球对地面的平均冲力为(g=10m/s2)( )
| A. | 30N | B. | 60N | C. | 80N | D. | 100N |
12.当汽车以某一速度通过拱形桥的最高点时,它对路面的压力( )
| A. | 一定等于零 | B. | 小于它的重力 | C. | 等于它的重力 | D. | 大于它的重力 |
 如图,半径为R的四分之一的光滑圆弧轨道,轨道下端与水平面相切,一质量为m的物体从顶端由静止沿轨道下滑,g=10m/s2 ,求在最低点时轨道受到的压力F.
如图,半径为R的四分之一的光滑圆弧轨道,轨道下端与水平面相切,一质量为m的物体从顶端由静止沿轨道下滑,g=10m/s2 ,求在最低点时轨道受到的压力F.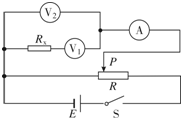 用如图所示的电路可同时测量定值电阻和电压表最小量程的内电阻.图中V1、V2为两块相同规格的多量程待测电压表,Rx为较大阻值的待测定值电阻,A为电流表,R为滑动变阻器,E为电源,S为电键.
用如图所示的电路可同时测量定值电阻和电压表最小量程的内电阻.图中V1、V2为两块相同规格的多量程待测电压表,Rx为较大阻值的待测定值电阻,A为电流表,R为滑动变阻器,E为电源,S为电键.