题目内容
12.当汽车以某一速度通过拱形桥的最高点时,它对路面的压力( )| A. | 一定等于零 | B. | 小于它的重力 | C. | 等于它的重力 | D. | 大于它的重力 |
分析 在最高点,重力和支持力的合力提供向心力,根据牛顿第二定律求出支持力的大小,再根据牛顿第三定律求出汽车通过桥最高点时对桥面的压力.
解答 解:汽车通过桥的最高点时受力如图,根据牛顿第二定律得:$mg-N=m\frac{{v}^{2}}{R}$
桥面对汽车的支持力:$N=mg-m\frac{{v}^{2}}{R}$
根据牛顿第三定律,汽车对桥面的压力:$N′=N=mg-m\frac{{v}^{2}}{R}<mg$
故选:B
点评 解决本题的关键搞清向心力的来源,运用牛顿第二定律进行求解,难度不大,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
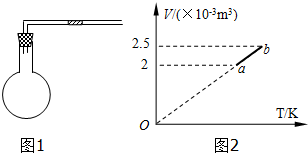
20. 如图所示,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场,磁场水平向外.磁极狭缝间某点的磁感应强度与该点到圆柱形磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度无初速释放,线圈在磁极狭缝间下落的过程中,线圈平面始终水平且保持与圆柱形磁极共轴.线圈被释放后( )
如图所示,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场,磁场水平向外.磁极狭缝间某点的磁感应强度与该点到圆柱形磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度无初速释放,线圈在磁极狭缝间下落的过程中,线圈平面始终水平且保持与圆柱形磁极共轴.线圈被释放后( )
 如图所示,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场,磁场水平向外.磁极狭缝间某点的磁感应强度与该点到圆柱形磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度无初速释放,线圈在磁极狭缝间下落的过程中,线圈平面始终水平且保持与圆柱形磁极共轴.线圈被释放后( )
如图所示,一个很长的竖直放置的圆柱形磁铁,产生一个辐射状的磁场,磁场水平向外.磁极狭缝间某点的磁感应强度与该点到圆柱形磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度无初速释放,线圈在磁极狭缝间下落的过程中,线圈平面始终水平且保持与圆柱形磁极共轴.线圈被释放后( )| A. | 线圈中没有感应电流,线圈做自由落体运动 | |
| B. | 在图1俯视图中,线圈中感应电流沿逆时针方向 | |
| C. | 线圈有最大速度,线圈半径越大,最大速度越小 | |
| D. | 线圈有最大速度,线圈半径越大,最大速度越大 |
7.决定惯性大小的因素是物体的( )
| A. | 速度 | B. | 质量 | C. | 体积 | D. | 密度 |
4.关于磁感应强度B,下列说法中正确的是( )
| A. | 磁场中某点B的大小,跟放在该点的试探电流元的情况有关 | |
| B. | 磁场中某点B的方向,跟该点处试探电流元所受磁场力方向一致 | |
| C. | 在磁场中某点试探电流元不受磁场力作用时,该点B值大小为零 | |
| D. | 在磁场中磁感线越密集的地方,B值越大 |
1.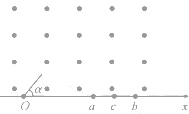 如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )
如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )
 如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )
如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )| A. | B粒子在磁场中的运动时间比A粒子在磁场中的运动时间长 | |
| B. | 粒子A、B在磁场中的运动时间相同 | |
| C. | 可以求出C粒子的质量 | |
| D. | C粒子在磁场中作圆周运动的半径一定比B粒子作圆周运动的半径小 |
2. 如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
 如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )| A. | cos3α=$\frac{q}{8Q}$ | B. | cos3α=$\frac{{q}^{2}}{{Q}^{2}}$ | C. | sin3α=$\frac{Q}{8q}$ | D. | sin3α=$\frac{{Q}^{2}}{{q}^{2}}$ |
 如图所示是物体做直线运动的v-t图象,由图可知:第1s与第3s的速度方向相反(填“相同”或“相反”),第2s的加速度大小10m/s2.
如图所示是物体做直线运动的v-t图象,由图可知:第1s与第3s的速度方向相反(填“相同”或“相反”),第2s的加速度大小10m/s2.