��Ŀ����
6������������Ĥ��������ӵĴ�С����ʵ���У�ʵ��ļ�Ҫ�������£�a����������Ĥ�����IJ������������ֽ�ϣ����������ڵķ��������ٸ��ݷ���ı߳������Ĥ�����S��
b��������ʯ��ۣ������ӷۣ���������ˮ���ϣ�
c����dz���е���Լ2cm���ˮ��
d����һ��������Һ����dz���У�
e������ܣ���ιܣ���С��Ͳ�е���1mL������Һ�����µ���ĵ���n�����һ��������Һ�����V0��
f�������ᱡĤ��״�ȶ�����������dz���ϣ��òʱʣ���ֱʣ��������ᱡĤ����״��
g�����ݽ�ʦ��������ƾ���Һ��Ũ�ȣ����һ����Һ�д���������V��
h������һ�δ���������V�ͱ�Ĥ���S�����������Ĥ�ĺ��d=$\frac{V}{S}$����Ϊ������ӵĴ�С��
�뽫����ʵ�鲽�谴������˳������egcbdfah��
���� �����ƺõ�����ƾ���Һ��ͨ����Ͳ���1�δ���Һ�������Ȼ��1�δ���Һ���������ӷ۵�dz�����ˮ���ϣ��ȴ���״�ȶ������������dz���ϣ��òʱ���������Ĥ����״�����������ᱡĤ�����IJ������������ֽ�ϣ�����������ȥ�����ڰ������һ����ͳ�Ƴ����ᱡĤ�����������1�δ���Һ���������1�δ���Һ�������ǡ�þ���������ӵ�ֱ����
��� �⣺����Ĥ������������ӵĴ�С��ʵ�鲽��Ϊ�����ƾƾ�������Һ����ʦ��ɣ��������Ʊ��������ⶨһ�ξƾ�������Һ�����v=$\frac{V}{N}$����dzˮ�̡��γ���Ĥ�������Ĥ��Ե��������Ĥ������������ֱ������ʵ�鲽��Ϊegcbdfah��
�ʴ�Ϊ��egcbdfah��
���� ���⿼�顰�õ�������Ĥ������Ӵ�С��ʵ���ʵ�鲽������ݴ������ѶȲ�����һ�������⣬�������ջ���֪ʶ������ȷ���⣻����ʱҪע�⣬VӦ���Ǵ��͵���������Ǿƾ�������Һ�������

��ϰ��ϵ�д�
 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
�����Ŀ
16��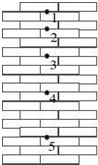 С�����ֱשǽijλ���ɾ�ֹ�ͷţ���Ƶ���������ͬһ��Ƭ�϶���ع⣬�õ���ͼʾ����Ƭ����֪���������ع��ʱ������ΪT��ÿ��ש�ĺ��Ϊd������ͼ����Ϣ������˵����ȷ���ǣ�������
С�����ֱשǽijλ���ɾ�ֹ�ͷţ���Ƶ���������ͬһ��Ƭ�϶���ع⣬�õ���ͼʾ����Ƭ����֪���������ع��ʱ������ΪT��ÿ��ש�ĺ��Ϊd������ͼ����Ϣ������˵����ȷ���ǣ�������
 С�����ֱשǽijλ���ɾ�ֹ�ͷţ���Ƶ���������ͬһ��Ƭ�϶���ع⣬�õ���ͼʾ����Ƭ����֪���������ع��ʱ������ΪT��ÿ��ש�ĺ��Ϊd������ͼ����Ϣ������˵����ȷ���ǣ�������
С�����ֱשǽijλ���ɾ�ֹ�ͷţ���Ƶ���������ͬһ��Ƭ�϶���ع⣬�õ���ͼʾ����Ƭ����֪���������ع��ʱ������ΪT��ÿ��ש�ĺ��Ϊd������ͼ����Ϣ������˵����ȷ���ǣ�������| A�� | ���ж�λ�á�1����С���ͷŵij�ʼλ�� | |
| B�� | �����С������ļ��ٶȴ�СΪa=$\frac{d}{4{T}^{2}}$ | |
| C�� | �����С����λ�á�3�����ٶȴ�СΪV=$\frac{7d}{T}$ | |
| D�� | �����֪�����ص��������ٶȣ��Ϳ�����֤С����������л�е���Ƿ��غ� |
17�������о�ƽ���˶�����ʵ��ʱ���ڰ�װʵ�������Ĺ����У�б��ĩ�˵����߱�����ˮƽ�ģ���������Ŀ���ǣ�������
| A�� | ��֤С��ɳ�ʱ���ٶ��ʵ� | B�� | ��֤С��ɳ�ʱ�ij��ٶȷ���ˮƽ | ||
| C�� | ��֤С���ڿ��е�ʱ��ÿ�ζ���� | D�� | ��֤С����˶��켣��һ�������� |
14����������ѧ���ɺͷ��Ӷ����ۣ�����˵����ȷ���ǣ�������
| A�� | �����˶�����Һ����ӵ��˶�����˵���˷���������ͣϢ���������˶� | |
| B�� | �ܷ����ݻ�����������ڵ����壬���¶����ߣ���������Ӷ����ڵ�λ����ϵ�ƽ������������ | |
| C�� | �ڶ���������Υ��������ѧ�ڶ����ɣ����Բ������Ƴ� | |
| D�� | ��������ѧ�ڶ����ɿ�֪�������ܹ��Ӹ������崫���������壬�������ܴӵ������崫���������� |
1�� ��֪����е����Ϊq�ľ�ֹ���ɣ���ѡȡ���������Զ���ĵ���Ϊ��ʱ������ɾ���Ϊr���ĵ���Ϊ��=$\frac{kq}{r}$��kΪ����������������ͼ��ʾ���������Ϊ+Q��-q�����ֵ������Ϊd���ֽ�һ���ӣ������Ϊe��������������ϵ�A�����Ը����ΪԲ�ġ��뾶ΪR�İ�Բ�ι켣ABC�Ƶ�C�㣬�����Ӵ�A��C�Ĺ����У�ϵͳ�����ܵı仯���Ϊ��������
��֪����е����Ϊq�ľ�ֹ���ɣ���ѡȡ���������Զ���ĵ���Ϊ��ʱ������ɾ���Ϊr���ĵ���Ϊ��=$\frac{kq}{r}$��kΪ����������������ͼ��ʾ���������Ϊ+Q��-q�����ֵ������Ϊd���ֽ�һ���ӣ������Ϊe��������������ϵ�A�����Ը����ΪԲ�ġ��뾶ΪR�İ�Բ�ι켣ABC�Ƶ�C�㣬�����Ӵ�A��C�Ĺ����У�ϵͳ�����ܵı仯���Ϊ��������
 ��֪����е����Ϊq�ľ�ֹ���ɣ���ѡȡ���������Զ���ĵ���Ϊ��ʱ������ɾ���Ϊr���ĵ���Ϊ��=$\frac{kq}{r}$��kΪ����������������ͼ��ʾ���������Ϊ+Q��-q�����ֵ������Ϊd���ֽ�һ���ӣ������Ϊe��������������ϵ�A�����Ը����ΪԲ�ġ��뾶ΪR�İ�Բ�ι켣ABC�Ƶ�C�㣬�����Ӵ�A��C�Ĺ����У�ϵͳ�����ܵı仯���Ϊ��������
��֪����е����Ϊq�ľ�ֹ���ɣ���ѡȡ���������Զ���ĵ���Ϊ��ʱ������ɾ���Ϊr���ĵ���Ϊ��=$\frac{kq}{r}$��kΪ����������������ͼ��ʾ���������Ϊ+Q��-q�����ֵ������Ϊd���ֽ�һ���ӣ������Ϊe��������������ϵ�A�����Ը����ΪԲ�ġ��뾶ΪR�İ�Բ�ι켣ABC�Ƶ�C�㣬�����Ӵ�A��C�Ĺ����У�ϵͳ�����ܵı仯���Ϊ��������| A�� | ����$\frac{2kQeR}{{{d^2}+{R^2}}}$ | B�� | ����$\frac{2kqeR}{{{d^2}-{R^2}}}$ | ||
| C�� | ����$\frac{2kqeR}{{{d^2}+{R^2}}}$ | D�� | ����$\frac{2kQeR}{{{d^2}-{R^2}}}$ |
11���������ǵ���ϵͳ���ҹ��������ƿ�������������ά���Ƕ�λ��ͨ��ϵͳ��CNSS�������ɺ�ı������ǵ���ϵͳ����5��ͬ�����Ǻ�30��һ�������ǣ��������е�5��ͬ�����ǣ�����˵������ȷ���ǣ�������
| A�� | ����һ��������ͬ�������� | |
| B�� | һ��λ�ڿռ�ͬһ����� | |
| C�� | �������еļ��ٶ�һ����ͬ | |
| D�� | �������е����ٶ�һ����С��7.9km/s |
18�� ��ͼ��ʾ�ĵ�·�У���������������G1��G2����㶼�ڿ̶������룬�������ӡ�+������������ʱ��ָ�����Ұڣ������ӡ�-������������ʱ��ָ������ڣ��ڵ�·��ͨ�ȶ��������ٶϿ���˲�䣬�����ĸ�˵������ʵ�ʣ�������
��ͼ��ʾ�ĵ�·�У���������������G1��G2����㶼�ڿ̶������룬�������ӡ�+������������ʱ��ָ�����Ұڣ������ӡ�-������������ʱ��ָ������ڣ��ڵ�·��ͨ�ȶ��������ٶϿ���˲�䣬�����ĸ�˵������ʵ�ʣ�������
 ��ͼ��ʾ�ĵ�·�У���������������G1��G2����㶼�ڿ̶������룬�������ӡ�+������������ʱ��ָ�����Ұڣ������ӡ�-������������ʱ��ָ������ڣ��ڵ�·��ͨ�ȶ��������ٶϿ���˲�䣬�����ĸ�˵������ʵ�ʣ�������
��ͼ��ʾ�ĵ�·�У���������������G1��G2����㶼�ڿ̶������룬�������ӡ�+������������ʱ��ָ�����Ұڣ������ӡ�-������������ʱ��ָ������ڣ��ڵ�·��ͨ�ȶ��������ٶϿ���˲�䣬�����ĸ�˵������ʵ�ʣ�������| A�� | G1ָ������ڣ�G2ָ�����Ұ� | B�� | G1ָ�����Ұڣ�G2ָ������� | ||
| C�� | G1��G2��ָ�붼����� | D�� | G1��G2��ָ�붼���Ұ� |
