题目内容
16．
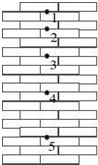小球从竖直砖墙某位置由静止释放，用频闪照相机在同一底片上多次曝光，得到了图示的照片．已知连续两次曝光的时间间隔均为T，每块砖的厚度为d．根据图中信息，下列说法正确的是（ ）| A． | 能判定位置“1”是小球释放的初始位置 | |
| B． | 能求出小球下落的加速度大小为a=$\frac{d}{4{T}^{2}}$ | |
| C． | 能求出小球在位置“3”的速度大小为V=$\frac{7d}{T}$ | |
| D． | 如果再知道当地的重力加速度，就可以验证小球下落过程中机械能是否守恒 |
分析 小球做的匀加速直线运动，根据相机的曝光的时间间隔相同，由匀变速直线运动的规律可以求得，根据a与g的关系判断机械能是否守恒．
解答 解：A、由于时间的间隔相同，所以3点瞬时速度的大小为2、4之间的平均速度的大小，所以V3=$\frac{x}{t}=\frac{7d}{2t}$，由图可以知道每两个相邻的点之间的距离差是一样的，所以小球做匀加速直线运动，由△x=at2 可知，a=$\frac{d}{{T}^{2}}$，根据V=V0+at可知点1的速度大小是V1=V3-2at=$\frac{3d}{2T}$，所以位置“1”不是小球释放的初始位置，故ABC错误；
D、如果知道当地重力加速度，比较a与g的大小，若a=g则下落过程中机械能守恒，故D正确．
故选：D
点评 中间时刻的瞬时速度等于这段位移的平均速度的大小，利用这个结论可以很容易的求得物体在某时刻的瞬时速度的大小，对于物理中的一些结论和推论在平时的学习中要掌握住并会用．
练习册系列答案
相关题目
6．
如图所示，边长为L的正方形单匝线圈abcd，其电阻为r，外电路的电阻为R，ab的中点和cd的中点的连线O′O恰好位于匀强磁场的边界线上，磁场的磁感应强度为B，若线圈从图示位置开始以角速度ω绕轴O′O匀速转动，则以下判断正确的是（ ）
如图所示，边长为L的正方形单匝线圈abcd，其电阻为r，外电路的电阻为R，ab的中点和cd的中点的连线O′O恰好位于匀强磁场的边界线上，磁场的磁感应强度为B，若线圈从图示位置开始以角速度ω绕轴O′O匀速转动，则以下判断正确的是（ ）| A． | 图示位置线圈中的感应电动势最大为Em=BL2ω | |
| B． | 闭合电路中感应电动势的瞬时值表达式为e=$\frac{1}{2}$BL2ωsinωt | |
| C． | 线圈从图示位置转过180°的过程中，流过电阻R的电荷量为q=$\frac{B{L}^{2}}{R+r}$ | |
| D． | 线圈转动一周的过程中，电阻R上产生的热量为Q=$\frac{π{B}^{2}ω{L}^{4}R}{4（R+r）^{2}}$ |
7．
如图，金属圆环a与均匀带正电的绝缘圆环b同心共面放置，当b绕圆心O点在其所在平面内顺时针加速旋转时，下列说法正确的是（ ）
如图，金属圆环a与均匀带正电的绝缘圆环b同心共面放置，当b绕圆心O点在其所在平面内顺时针加速旋转时，下列说法正确的是（ ）| A． | 圆环a中有顺时针方向的感应电流 | B． | 圆环a中有逆时针方向的感应电流 | ||
| C． | 圆环a具有向内收缩的趋势 | D． | 圆环a具有向四周扩张的趋势 |
4．
如图所示，一质量为M，半径为0.1m的光滑大圆环，用一细轻杆固定在竖直平面内，套在大圆环上质量为m的小环（可视为质点），从大环的最高处由静止滑下，取重力加速度大小g=10m/s2，当小环滑到大环的最低点时，大环对轻杆拉力的大小为Mg+5mg，则在最低点时，小环的速度大小为（ ）
如图所示，一质量为M，半径为0.1m的光滑大圆环，用一细轻杆固定在竖直平面内，套在大圆环上质量为m的小环（可视为质点），从大环的最高处由静止滑下，取重力加速度大小g=10m/s2，当小环滑到大环的最低点时，大环对轻杆拉力的大小为Mg+5mg，则在最低点时，小环的速度大小为（ ）| A． | $\sqrt{6}$m/s | |
| B． | $\sqrt{5}$m/s | |
| C． | 2m/s | |
| D． | 因为M、m未知，所以不能求出小环的速度大小 |
如图所示，货车正在平直公路上以a1=0.2m/s2的加速度启动，同时，一只壁虎从静止开始以a2=0.15 m/s2的加速度在货车壁上向上匀加速爬行．则：
1．真空中两个静止的点电荷，它们之间的库仑力为F．若它们的电荷量都减小为原来的一半，距离增大为原来的2倍，它们之间的库仑力变为（ ）
| A． | F | B． | 8F | C． | $\frac{1}{8}$F | D． | $\frac{1}{16}$F |
8．
美国太空总署用火箭和卫星撞击月球来探测月球表面是否存在水分．据天文学家测量，月球的半径约为1800km，月球表面的重力加速度约为地球表面重力加速度的$\frac{1}{6}$，地球表面重力加速度g取10m/s2，万有引力常量G=6.67×10-11N•m2/kg2，下列说法正确的是（ ）
美国太空总署用火箭和卫星撞击月球来探测月球表面是否存在水分．据天文学家测量，月球的半径约为1800km，月球表面的重力加速度约为地球表面重力加速度的$\frac{1}{6}$，地球表面重力加速度g取10m/s2，万有引力常量G=6.67×10-11N•m2/kg2，下列说法正确的是（ ）| A． | 卫星撞月前应先在原绕月轨道上减速 | |
| B． | 卫星撞月前应先在原绕月轨道上加速 | |
| C． | 月球的第一宇宙速度大于2 km/s | |
| D． | 可算出月球的质量约为8×1022kg |
