题目内容
3.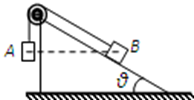 如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好保持静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块各自到达水平地面( )
如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好保持静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块各自到达水平地面( )| A. | 两物块动能变化量相同 | B. | A物体比B物体先到达水平地面 | ||
| C. | 重力势能的变化量相同 | D. | 重力做功的平均功率相同 |
分析 剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,机械能守恒,重力势能变化量等于重力所做的功,重力做功的平均功率等于重力做功与时间的比值.
解答 解:AC、刚开始AB处于静止状态,由平衡知识可知:mBgsinθ=mAg,则mB>mA,由动能定理可得:mgh=$\frac{1}{2}$mv2,解得:v=$\sqrt{2gh}$,因为h相同,落地速率相等,又因为质量不等,所以两物块动能变化量不同,重力势能的变化量也不同,故AC错误;
B、初始时刻,A、B处于同一高度并恰好处于静止状态.当剪断后,A的合力为mAg,加速度为g,B的合力为mBgsinθ,根据牛顿第二定律可知B的加速度为gsinθ,对A,由h=$\frac{1}{2}$gt2,得tA=$\sqrt{\frac{2h}{g}}$;对B,由$\frac{h}{sinθ}$=$\frac{1}{2}$gsinθtB2,则得 tB=$\frac{1}{sinθ}$$\sqrt{\frac{2h}{g}}$,可知tA<tB,所以A物体比B物体先到达水平地面,故B正确;
D、A重力做功的平均功率为:$\overline{{P}_{A}}$=$\frac{{m}_{A}gh}{{t}_{A}}$=mAgh$\sqrt{\frac{g}{2h}}$;B重力做功的平均功率为:$\overline{{P}_{B}}$=$\frac{{m}_{B}gh}{{t}_{B}}$=mBgsinθ$\sqrt{\frac{g}{2h}}$=mAgh$\sqrt{\frac{g}{2h}}$,所以重力做功的平均功率相等,故D正确.
故选:BD.
点评 重力做功决定重力势能的变化与否,若做正功,则重力势能减少;若做负功,则重力势能增加,重力做功的平均功率等于重力做功与时间的比值,难度适中.

 如图所示,竖直方向的匀强磁场中有一个矩形闭合导线框.在下列情况中,线框中能产生感应电流的是(线框始终全部在磁场中)( )
如图所示,竖直方向的匀强磁场中有一个矩形闭合导线框.在下列情况中,线框中能产生感应电流的是(线框始终全部在磁场中)( )| A. | 保持线框平面始终与磁场垂直,线框在磁场中上下运动 | |
| B. | 保持线框平面始终与磁场垂直,线框在磁场中左右运动 | |
| C. | 线框绕AC轴匀速转动,当线框平面与磁场垂直时 | |
| D. | 线框绕AC轴匀速转动,当线框平面与磁场平行时 |
| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
| A. | F1=$\frac{GMm}{{R}^{2}}$ | B. | F2=$\frac{R}{R-h}$F1 | C. | F2=F1-m$\frac{{4π}^{2}}{{T}^{2}}$R | D. | F1=m$\frac{{4π}^{2}}{{T}^{2}}$R |
| A. | 动能可以为负值 | |
| B. | 一定质量的物体动能变化时,速度一定变化,速度变化时,动能也一定变化 | |
| C. | 动能不变的物体,一定处于平衡状态 | |
| D. | 描述物体的动能时,其实也是需要选择参考系的,一般选地面或相对地面静止的物体 |
 如图所示,在水平面上一轻质弹簧竖直放置,在它正上方一小球自由落下,不空气阻力,从小球接触弹簧到速度减为零的过程中 ( )
如图所示,在水平面上一轻质弹簧竖直放置,在它正上方一小球自由落下,不空气阻力,从小球接触弹簧到速度减为零的过程中 ( )| A. | 小球的动能不断减小 | B. | 小球所受的合力不断增大 | ||
| C. | 弹簧的弹性势能不断增大 | D. | 小球的机械能守恒 |
 同学采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图,假设他的质量为m,在起跑后前进的距离s内,重心上升高度为h,获得的速度为v,阻力做功为W阻,则在此过程中:
同学采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图,假设他的质量为m,在起跑后前进的距离s内,重心上升高度为h,获得的速度为v,阻力做功为W阻,则在此过程中:
 如图所示,光滑、半圆形轨道竖直放置,轨道半径R=80cm,其底部与粗糙、水平轨道相接,连接点为P,一小球A以一定的初速度沿水平轨道向左运动,测得小球A经过N点时的速度vN=8m/s,小球A经过水平轨道后沿圆轨道的内壁运动到最高点M,测得经过M点时对轨道的压力为0.5N,小球A的质量m=50g,重力加速度度g=10m/s2.求:
如图所示,光滑、半圆形轨道竖直放置,轨道半径R=80cm,其底部与粗糙、水平轨道相接,连接点为P,一小球A以一定的初速度沿水平轨道向左运动,测得小球A经过N点时的速度vN=8m/s,小球A经过水平轨道后沿圆轨道的内壁运动到最高点M,测得经过M点时对轨道的压力为0.5N,小球A的质量m=50g,重力加速度度g=10m/s2.求: