题目内容
12. 如图所示,一竖直放置、半径为R的粗糙半圆形轨道BC与一水平面AB在B点相连,B点为轨道的最低点,C点为轨道的最高点.一质量为m的小球以初速度v0从B点进入竖直圆轨道BC,沿着圆轨道运动并恰好通过最高点C,然后做平抛运动.求:
如图所示,一竖直放置、半径为R的粗糙半圆形轨道BC与一水平面AB在B点相连,B点为轨道的最低点,C点为轨道的最高点.一质量为m的小球以初速度v0从B点进入竖直圆轨道BC,沿着圆轨道运动并恰好通过最高点C,然后做平抛运动.求:(1)小球平抛后落地点D距B点的水平距离和到达D点时重力的功率;
(2)小球由B点沿着半圆轨道到达C点过程中,克服轨道摩擦阻力所做的功.
分析 (1)抓住小球恰好通过最高点C,根据牛顿第二定律求出C点的速度,根据高度求出平抛运动的时间,结合C点的速度和时间求出平抛运动的水平位移.根据D点的竖直分速度,求出重力的瞬时功率.
(2)对B到C的过程运用动能定理,求出克服摩擦力做功的大小.
解答 解:(1)小球恰好通过最高点C,有:mg=$m\frac{{{v}_{C}}^{2}}{R}$,
解得:${v}_{C}=\sqrt{gR}$,
根据2R=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{4R}{g}}$,
则落地点D距B点的水平距离为:x=${v}_{C}t=\sqrt{gR}×\sqrt{\frac{4R}{g}}=2R$.
到达D点时竖直分速度${v}_{Dy}=\sqrt{2g•2R}$=$2\sqrt{gR}$,则重力的功率为:P=$mg{v}_{Dy}=2mg\sqrt{gR}$.
(2)对B到C的过程,根据动能定理得:$-mg•2R-{W}_{f}=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,
解得:Wf=$\frac{1}{2}m{{v}_{0}}^{2}-\frac{5}{2}mgR$.
答:(1)小球平抛后落地点D距B点的水平距离为2R,到达D点时重力的功率为$2mg\sqrt{gR}$;
(2)小球由B点沿着半圆轨道到达C点过程中,克服轨道摩擦阻力所做的功为$\frac{1}{2}m{{v}_{0}}^{2}-\frac{5}{2}mgR$.
点评 本题考查了平抛运动、圆周运动与牛顿定律、动能定理的综合,知道平抛运动在水平方向和竖直方向上的运动规律,以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
相关题目
6.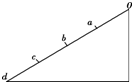 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 在斜面上运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
3.最早发表有关碰撞问题研究成果的是( )
| A. | 牛顿 | B. | 伽利略 | C. | 惠更新 | D. | 马尔西 |
7. 如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
 如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )| A. | 电场线与ac直线平行 | B. | 电场方向与ac直线垂直 | ||
| C. | b点电势为3V | D. | b、d位于同一等势面上 |
1.下列说法正确的是( )
| A. | 电容器的电容越大,它能容纳的电荷量就越多 | |
| B. | 电场中某一空间区域电势处处相等,则该区域内场强处处为0 | |
| C. | 电场强度为零的地方,电势必定为零 | |
| D. | 法拉第通过对电现象和磁现象的研究,首先提出了场的概念 |
2.某实验小组想通过实验研究水果电池的电动势和内电阻.他们制作了一个苹果电池进行研究,了解到水果电池的内电阻可能比较大,因此设计了一个如图1所示的实物电路进行测量.

(1 )请按图中所示实物图在图2的方框内画出电路图 (电源用“ ”表示).
”表示).
(2 )测定水果电池的电动势和内阻,所用的器材有:
①苹果电池 E:电动势约为 1V;
②电压表 V:量程 1V,内阻 R V=3kΩ;
③电阻箱 R:最大阻值 9999Ω;
④开关 S,导线若干.
(3 )实验步骤如下:
①按电路图连接电路 (为电路安全,先将电阻箱的电阻调到最大值);
②闭合开关 S,多次调节电阻箱,记下电压表的示数 U 和电阻箱相应的阻值R,并计算出对应的$\frac{1}{R}$与$\frac{1}{U}$的值,如下表所示;
③以$\frac{1}{R}$与$\frac{1}{U}$为纵坐标,$\frac{1}{U}$-$\frac{1}{R}$为横坐标,将计算出的数据描绘在坐标纸内,做出$\frac{1}{U}$-$\frac{1}{R}$ 图线;
④计算得出水果电池的电动势和内阻.
请回答下列问题:
ⅰ.实验得到的部分数据如上表所示,其中当电阻箱的电阻 R=2000Ω 时电压表的示数如图3所示.读出数据,完成上表.
答:①0.37,②2.7.
ⅱ.请根据实验数据在图中做出$\frac{1}{U}$-$\frac{1}{R}$ 图线
ⅲ.根据$\frac{1}{U}$-$\frac{1}{R}$图线求得该水果电池的电动势 E=0.9V,内阻r=1.8×103Ω.

(1 )请按图中所示实物图在图2的方框内画出电路图 (电源用“
 ”表示).
”表示).(2 )测定水果电池的电动势和内阻,所用的器材有:
①苹果电池 E:电动势约为 1V;
②电压表 V:量程 1V,内阻 R V=3kΩ;
③电阻箱 R:最大阻值 9999Ω;
④开关 S,导线若干.
(3 )实验步骤如下:
①按电路图连接电路 (为电路安全,先将电阻箱的电阻调到最大值);
②闭合开关 S,多次调节电阻箱,记下电压表的示数 U 和电阻箱相应的阻值R,并计算出对应的$\frac{1}{R}$与$\frac{1}{U}$的值,如下表所示;
| R/Ω | 9000 | 6000 | 5000 | 4000 | 3000 | 2000 |
| R-1/10-4Ω-1 | 1.11 | 1.67 | 2.0 | 2.5 | 3.33 | 5.0 |
| U/V | 0.53 | 0.50 | 0.48 | 0.46 | 0.43 | ① |
| U-1/V-1 | 1.9 | 2.0 | 2.1 | 2.2 | 2.3 | ② |
④计算得出水果电池的电动势和内阻.
请回答下列问题:
ⅰ.实验得到的部分数据如上表所示,其中当电阻箱的电阻 R=2000Ω 时电压表的示数如图3所示.读出数据,完成上表.
答:①0.37,②2.7.
ⅱ.请根据实验数据在图中做出$\frac{1}{U}$-$\frac{1}{R}$ 图线
ⅲ.根据$\frac{1}{U}$-$\frac{1}{R}$图线求得该水果电池的电动势 E=0.9V,内阻r=1.8×103Ω.
 物体做匀速圆周运动时,向心力与哪些因素有关?某同学通过下面实验探究,获得体验.
物体做匀速圆周运动时,向心力与哪些因素有关?某同学通过下面实验探究,获得体验.