题目内容
2.跳伞运动员跳离飞机后先做自由落体运动,速度达到v时,打开降落伞,以大小为a的加速度做匀减速运动,到达地面时速度为nv(0<n<1),重力加速度为g.则( )| A. | 自由落体时间与减速时间之比为a:(1-n)g | |
| B. | 自由落体的距离与减速运动的距离之比为a:g | |
| C. | 自由落体的平均速度小于减速运动的平均速度 | |
| D. | 全程平均速度大于$\frac{v}{2}$ |
分析 根据自由落体运动得速度时间公式和速度位移公式求解自由落体运动的时间和位移,根据匀变速直线运动时间公式和速度位移公式求解匀减速运动的时间和位移,根据匀变速直线运动平均速度$\overline{v}=\frac{{v}_{0}+v}{2}$求解平均速度.
解答 解:A、自由落体时间${t}_{1}=\frac{v}{g}$,匀减速运动的时间${t}_{2}=\frac{nv-v}{-a}=(1-n)\frac{v}{a}$,则$\frac{{t}_{1}}{{t}_{2}}=\frac{\frac{v}{g}}{(1-n)\frac{v}{a}}=\frac{a}{(1-n)g}$,故A正确;
B、自由落体的距离${h}_{1}=\frac{{v}^{2}}{2g}$,减速运动的距离${h}_{2}=\frac{{v}^{2}-(nv)^{2}}{2a}$,则$\frac{{h}_{1}}{{h}_{2}}=\frac{a}{g(1-{n}^{2})}$,故B错误;
C、自由落体的平均速度$\overline{{v}_{1}}=\frac{v}{2}$,减速运动的平均速度$\overline{{v}_{2}}=\frac{v+nv}{2}$,所以$\overline{{v}_{2}}>\overline{{v}_{1}}$,故C正确;
D、自由落体的平均速度为$\frac{v}{2}$,减速运动的平均速度大于$\frac{v}{2}$,所以全程平均速度大于$\frac{v}{2}$,故D正确.
故选:ACD
点评 本题主要考查了匀变速直线运动基本公式的直接应用,知道自由落体运动是初速度为零,加速度为g的匀加速直线运动,难度不大,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
18.用电梯将货物从六楼送到一楼的过程中,货物的v-t图象如图所示.下列说法正确的是( )


| A. | 货物在 第10s内加速度为-2m/s2 | B. | 货物在 10s内的平均速度是1.7m/s | ||
| C. | 前2s内货物处于超重状态 | D. | 最后1s内货物只受重力作用 |
13.下列关于速度与加速度的说法中正确的是( )
| A. | 速度变化越大,加速度一定越大 | |
| B. | 速度变化方向为正,加速度方向可能为负 | |
| C. | 速度变化率越小,加速度越小 | |
| D. | 加速度增大时,速度一定增大 |
10.下列说法中正确的是( )
| A. | 牛顿通过理想斜面实验发现力不是维持物体运动的原因 | |
| B. | 千克、秒、米都是基本单位 | |
| C. | 法国科学家笛卡尔指出:如果物体没有受到力的作用,它将继续以同一速度沿同一 直线运动 | |
| D. | 力、速度、加速度的单位都是导出中单位 |
17.如图,当滑动变阻器的滑动头向左滑动时,A、B两灯亮度的变化情况为( )


| A. | 都变亮 | B. | 都变暗 | C. | A灯变亮,B灯变暗 | D. | A灯变暗,B灯变亮 |
7. 如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,两轻绳能够承受的最大拉力相同,则( )
如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,两轻绳能够承受的最大拉力相同,则( )
 如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,两轻绳能够承受的最大拉力相同,则( )
如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,两轻绳能够承受的最大拉力相同,则( )| A. | FA大于FB | |
| B. | FA、FB的合力等于mg | |
| C. | 调节悬点A的位置,可使FA、FB的合力大于mg | |
| D. | 无论如何调节悬点A的位置,FA、FB都不可能大于mg |
14.在电磁学理论建立和发展的过程中,有许多伟大的科学家做出了贡献.关于科学家及其贡献,下列说法正确的是( )
| A. | 卡文迪许利用卡文迪许扭秤首先较准确的测定了静电力常量 | |
| B. | 洛仑兹通过实验测定了磁场对电流的作用力 | |
| C. | 库仑在前人研究的基础上提出了真空中点电荷的相互作用规律 | |
| D. | 安培成功地发现了电能“生”磁 |
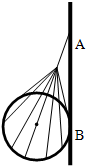 在光滑墙壁上用网兜把足球挂在A点,足球与墙面的接触点为B.足球的质量为0.4kg,绳与墙壁的夹角为37°.(sin37°=0.6,cos37°=0.8)
在光滑墙壁上用网兜把足球挂在A点,足球与墙面的接触点为B.足球的质量为0.4kg,绳与墙壁的夹角为37°.(sin37°=0.6,cos37°=0.8)