题目内容
1.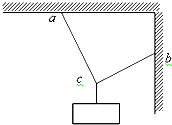 用三根轻绳将质量为m的物块悬挂在空中,如图所示,已知绳ac和bc与竖直方向的夹角分别为30°和60°,则ac与bc绳中的拉力分别为多少?(分别用力的合成和力的分解两种方法求解)
用三根轻绳将质量为m的物块悬挂在空中,如图所示,已知绳ac和bc与竖直方向的夹角分别为30°和60°,则ac与bc绳中的拉力分别为多少?(分别用力的合成和力的分解两种方法求解)
分析 c点进行受力分析,然后根据平衡条件和三角函数表示出力与力之间的关系.
解答 解:(1)合成法:
对结点C受力分析,受到三根绳子拉力,将Fa和Fb合成为F,
根据三力平衡得出:F=Fc=mg
已知ac和bc与竖直方向的夹角分别为30°和60°,所以α=30°
根据三角函数关系得出:
Fa=F•cosα=$\frac{\sqrt{3}}{2}$mg
Fb=F•sinα=$\frac{1}{2}$mg
(2)分解法:
以结点c为研究对象,受到三个拉力作用,作出力图.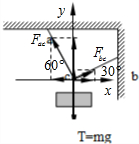 整个装置静止,则重物对c点拉力F等于重物的重力,根据平衡条件得:
整个装置静止,则重物对c点拉力F等于重物的重力,根据平衡条件得:
x轴:Faccos60°=Fbccos30° …①
y轴:Facsin60°+Fbcsin30°=mg…②
由①②两式联立可得ac绳和bc绳中的拉力Fac和Fbc分别为:
Fac=$\frac{\sqrt{3}}{2}$mg
Fbc=$\frac{1}{2}$mg
答:ac与bc绳中的拉力分别为$\frac{\sqrt{3}}{2}$mg和$\frac{1}{2}$mg.
点评 该题的关键在于能够对结点c进行受力分析,利用平衡状态条件解决问题;力的计算离不开几何关系和三角函数.

练习册系列答案
相关题目
6.如图是甲乙两物体在同一直线上做匀速直线运动的x-t图象,由图象可以判断( )


| A. | 乙比甲早运动了t1秒 | B. | t=t1时,两物体相距x0米 | ||
| C. | t=t2时,两物体相遇 | D. | t=t3时,两物体相距最远 |
13.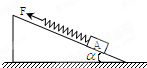 如图,倾角为α的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态.在这一过程中( )
如图,倾角为α的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态.在这一过程中( )
 如图,倾角为α的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态.在这一过程中( )
如图,倾角为α的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态.在这一过程中( )| A. | 弹簧的伸长量为 $\frac{F-mgsinα}{k}$ | |
| B. | 弹簧的伸长量为 $\frac{mgsinα}{k}$ | |
| C. | 斜面体受地面的支持力大小等于(m+M)g | |
| D. | 斜面体受地面的静摩擦力大小等于Fcosα |
11.对于连入电路的不同灯泡,亮度大的灯泡是( )
| A. | 通过的电流大的灯泡 | B. | 两端电压大的灯泡 | ||
| C. | 电阻大的灯泡 | D. | 消耗电功率大的灯泡 |

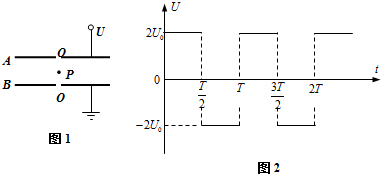
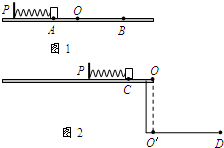 为测量小木块与水平桌面之间的动摩擦因数,某实验小组进行了以下实验操作:
为测量小木块与水平桌面之间的动摩擦因数,某实验小组进行了以下实验操作: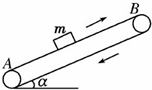 如图所示,白色的传送带两轮A、B的距离L=15m,传送带以恒定速度v=2m/s顺时针运动,现将一质量为m的小煤块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,设小煤块在运动过程中的质量不变,传送带的倾角为θ=370,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,白色的传送带两轮A、B的距离L=15m,传送带以恒定速度v=2m/s顺时针运动,现将一质量为m的小煤块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,设小煤块在运动过程中的质量不变,传送带的倾角为θ=370,g取10m/s2,sin37°=0.6,cos37°=0.8,求: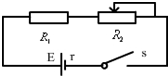 如图所示,已知电源电动势E=6V,内电阻r=2Ω,定值电阻R1=1Ω,滑动变阻器R2的最大值R2max=10Ω,求:
如图所示,已知电源电动势E=6V,内电阻r=2Ω,定值电阻R1=1Ω,滑动变阻器R2的最大值R2max=10Ω,求: