题目内容
2. 如图所示,实线为某时刻的波形图象,虚线是经过0.4s的波形图象,若T<0.4s<3T.则下列说法正确的是( )
如图所示,实线为某时刻的波形图象,虚线是经过0.4s的波形图象,若T<0.4s<3T.则下列说法正确的是( )| A. | 波的传播速度最小为17.5m/s | B. | 波的传播速度最大为22.5m/s | ||
| C. | 最大频率为5.625Hz | D. | 最小频率为3.125Hz |
分析 从题干信息不能确定横波的传播方向,故解题时要分两种情况讨论.①若波的传播方向沿着x轴正方向,设波传播的距离为△x1,将可能的△x1表示出来,根据T<△t<3T得到 λ<△x1<3λ,计算出可能的△x1,计算出对应的波速和频率;②若波的传播方向沿着x轴负方向,设波传播的距离为△x2,将可能的△x2表示出来,根据T<△t<3T得到 λ<△x2<3λ,计算出可能的△x2,计算出对应的波速和频率.
解答 解:A、题干中实线波形变化成虚线波形用时△t=0.4s,由图可知λ=4m.分两种情况讨论.
①若波的传播方向沿着x轴正方向,设波传播的距离为△x1,
则△x1=($\frac{1}{4}λ+{n}_{1}λ$)=(4n+1)m(n1=0,1,2,3…),
因为T<△t<3T,故 λ<△x1<3λ,即λ<4n1+1<3λ,所以n1=1,2.
当n1=1时,△x1=5m,已知△t=0.4s,${v}_{1}=\frac{△{x}_{1}}{△t}=12.5m/s$,${f}_{1}=\frac{{v}_{1}}{λ}=3.125m/s$;
当n1=2时,$△{x}_{1}^{'}=9m$,${v}_{1}^{'}=22.5m/s$,${f}_{1}^{'}=5.625m/s$;
②若波的传播方向沿着x轴负方向,设波传播的距离为△x2,
则$△{x}_{2}=(\frac{3}{4}λ+{n}_{2}λ)=(4{n}_{2}+3)\\;m$ m (n2=1,2,3…),
因为T<△t<3T,故 λ<△x2<3λ,△t=0.4s,所以 n2=1,2.
当n2=1时,v2=17.5m/s,f2=4.375m/s;
当n2=2时,$△{x}_{2}^{'}=11m$,△t=0.4s,${v}_{2}^{'}=27.5m/s$,${f}_{2}^{'}=6.875m/s$.
故最小的波速为12.5m/s,故A错误;
B、从A选项的讨论可知,最大波速为27.5m/s,故B错误.
C、从A选项的讨论可知,最大频率为6.875Hz,故C错误.
D、从A选项的讨论可知,最小频率为3.125Hz,故D正确.
故选:D
点评 此类型的题目,解题方法一般比较固定,分两种情况讨论;
讨论:①若波的传播方向沿着x轴正方向,设波传播的距离为△x1,
则△x1=($\frac{1}{4}λ+{n}_{1}λ$)=(4n+1)m(n1n1=1和n2=2=0,1,2,3…),
因为T<△t<3T,故 λ<△x1<3λ,即λ<4n1+1<3λ,解出n1=1,2,再将n1=1和n2=2代入计算;
②②若波的传播方向沿着x轴负方向,设波传播的距离为△x2,
则$△{x}_{2}=(\frac{3}{4}λ+{n}_{2}λ)=(4{n}_{2}+3)\\;m$ m (n2=1,2,3…),
因为T<△t<3T,故 λ<△x2<3λ,△t=0.4s,所以 n2=1,2.再将n1=1和n2=2代入计算.

 小学课时特训系列答案
小学课时特训系列答案| A. | E=$\frac{F}{q}$中的场强E是电荷q产生的 | B. | E=$\frac{F}{q}$和E=$\frac{kQ}{{r}^{2}}$都只对点电荷适用 | ||
| C. | E=$\frac{F}{q}$中的F表示单位正电荷的受力 | D. | E=$\frac{kQ}{{r}^{2}}$中的场强E是电荷Q产生的 |
| A. | 加速度和速度都变化,但物体所受合力不变 | |
| B. | 匀速圆周运动是匀变速运动,其加速度恒定不变 | |
| C. | 合外力方向不一定垂直于速度方向,且不一定指向圆心 | |
| D. | 匀速圆周运动不是匀速运动,合外力方向一定指向圆心 |
| A. | 水附着层的分子比内部密集,表现为浸润 | |
| B. | 水附着层的分子比内部稀疏,表现为浸润 | |
| C. | 水银附着层的分子比内部密集,表现为浸润 | |
| D. | 水银附着层的分子比内部稀疏,表现为不浸润 |
 如图所示,图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1处的质点,Q是平衡位置为=4m处的质点,图乙为质点Q的振动图象,则( )
如图所示,图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1处的质点,Q是平衡位置为=4m处的质点,图乙为质点Q的振动图象,则( )| A. | 该波沿x轴向右传播 | |
| B. | t=0.10s时,质点P的速度方向为负方向 | |
| C. | t=0.10s时,质点P的加速度方向为正方向 | |
| D. | 若这列波的波源正在远离观察者,则观察者接收到的频率小于波源发出的频率 |
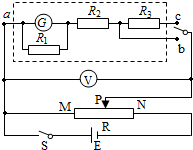 某同学改装和校准电压表的电路图如图所示,图中虚线框内是电压表的改装电路.
某同学改装和校准电压表的电路图如图所示,图中虚线框内是电压表的改装电路. 对改装表3V挡的不同刻度进行校准.所用电池的电动势E为5V;滑动变阻器R有两种规格,最大阻值分别为50Ω和5kΩ.为了方便实验中调节电压,图中R应选用最大阻值为50Ω的滑动变阻器.
对改装表3V挡的不同刻度进行校准.所用电池的电动势E为5V;滑动变阻器R有两种规格,最大阻值分别为50Ω和5kΩ.为了方便实验中调节电压,图中R应选用最大阻值为50Ω的滑动变阻器. 如图所示,一平板车静止在水平地面上,一货箱(可视为质点)放置一平板车右端,货箱离车后端的距离为l,某时刻平板车开始做a=4m/s2的匀加速直线运动,速度达到6m/s后匀速行驶,已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2,为使货箱不从平板车上掉下来,货箱离车后端的距离l应满足什么条件?
如图所示,一平板车静止在水平地面上,一货箱(可视为质点)放置一平板车右端,货箱离车后端的距离为l,某时刻平板车开始做a=4m/s2的匀加速直线运动,速度达到6m/s后匀速行驶,已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2,为使货箱不从平板车上掉下来,货箱离车后端的距离l应满足什么条件? 两个小球固定在一根长为L的轻杆两端,绕杆上的O点做圆周运动,如图所示.当小球1的速度为v1时,小球2的速度为v2,则转轴O到小球2的距离是$\frac{{v}_{2}}{{v}_{1}+{v}_{2}}$L.
两个小球固定在一根长为L的轻杆两端,绕杆上的O点做圆周运动,如图所示.当小球1的速度为v1时,小球2的速度为v2,则转轴O到小球2的距离是$\frac{{v}_{2}}{{v}_{1}+{v}_{2}}$L.