题目内容
20. 如图,轨道的AB段为一半径R=0.2m的光滑$\frac{1}{4}$圆,BC高h=5m,CD水平.一质量为0.2kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,之后离开B点做平抛运动(g=10m/s2),求:
如图,轨道的AB段为一半径R=0.2m的光滑$\frac{1}{4}$圆,BC高h=5m,CD水平.一质量为0.2kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,之后离开B点做平抛运动(g=10m/s2),求:(1)小球在CD 轨道上的落点到C 的水平距离;
(2)小球到达B 点时对圆轨道的压力大小?
(3)如果在如图虚线位置放一个倾角θ=37°的斜面,那么小球离开B点后第一次落在斜面上的位置距B多远?
分析 (1)根据高度求出平抛运动的时间,结合B点的速度求出落地点到C的水平距离.
(2)根据牛顿第二定律求出在B点的支持力,结合牛顿第三定律求出小球对B点的压力.
(3)根据竖直位移和水平位移的关系求出平抛运动的时间,从而求出水平位移,结合平行四边形定则求出小球离开B点第一次落在斜面上的位置距离B点的距离.
解答 解:(1)设小球平抛时间为t1,落地点到C点距离为s
竖直:h=$\frac{1}{2}g{{t}_{1}}^{2}$得:${t}_{1}=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×5}{10}}s=1s$,
水平位移:s=vBt1=2×1m=2m.
(2)根据牛顿第二定律得:$F-mg=m\frac{{v}^{2}}{R}$,
解得:F=mg+$m\frac{{v}^{2}}{R}$=$2+0.2×\frac{4}{0.2}$N=6N.
由牛顿第三定律知,小球对圆形轨道的压力大小为6N,方向竖直向下.
(3)设小球落点距B为L,时间为t
Lcosθ=vt,
Lsinθ=$\frac{1}{2}g{t}^{2}$
代入数据解得:t=0.3s,L=0.75m.
答:(1)小球在CD 轨道上的落点到C 的水平距离为2m;
(2)小球到达B 点时对圆轨道的压力大小为6N;
(3)小球离开B点后第一次落在斜面上的位置距B为0.75m.
点评 本题考查了平抛运动和圆周运动的综合运用,知道圆周运动向心力的来源以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
相关题目
10.对做圆周运动的物体所受的向心力说法正确的是( )
| A. | 因向心力总是沿半径指向圆心,且大小不变,故向心力是一个恒力 | |
| B. | 向心力和向心加速度的方向都是不变的 | |
| C. | 向心力是物体所受的合外力 | |
| D. | 因向心力指向圆心,且与线速度方向垂直,所以它不能改变线速度的大小 |
11.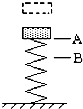 一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示.在A点物体开始与弹簧接触,到B点时物体速度为零,然后被弹回.不计空气阻力,下列说法中正确的是( )
一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示.在A点物体开始与弹簧接触,到B点时物体速度为零,然后被弹回.不计空气阻力,下列说法中正确的是( )
 一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示.在A点物体开始与弹簧接触,到B点时物体速度为零,然后被弹回.不计空气阻力,下列说法中正确的是( )
一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示.在A点物体开始与弹簧接触,到B点时物体速度为零,然后被弹回.不计空气阻力,下列说法中正确的是( )| A. | 物体从A下降到B的过程中,动能不断变小 | |
| B. | 物体从B上升到A的过程中,动能不断变大 | |
| C. | 物体从A下降到B和从B上升到A的过程中,加速度都是先增大后减小 | |
| D. | 物体在AB之间某点时,系统的重力势能与弹性势能之和最小 |
8.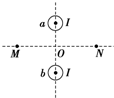 有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图中所示的平面内,O点为两根导线连线的中点,M、N为两根导线附近的两点,它们在两导线连线的中垂线上,且与O点的距离相等.若两导线中通有大小相等、方向相同的恒定电流I,则关于线段MN上各点的磁感应强度的说法中正确的是( )
有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图中所示的平面内,O点为两根导线连线的中点,M、N为两根导线附近的两点,它们在两导线连线的中垂线上,且与O点的距离相等.若两导线中通有大小相等、方向相同的恒定电流I,则关于线段MN上各点的磁感应强度的说法中正确的是( )
 有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图中所示的平面内,O点为两根导线连线的中点,M、N为两根导线附近的两点,它们在两导线连线的中垂线上,且与O点的距离相等.若两导线中通有大小相等、方向相同的恒定电流I,则关于线段MN上各点的磁感应强度的说法中正确的是( )
有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图中所示的平面内,O点为两根导线连线的中点,M、N为两根导线附近的两点,它们在两导线连线的中垂线上,且与O点的距离相等.若两导线中通有大小相等、方向相同的恒定电流I,则关于线段MN上各点的磁感应强度的说法中正确的是( )| A. | M点和N点的磁感应强度大小相等,方向相同 | |
| B. | M点和N点的磁感应强度大小相等,方向相反 | |
| C. | 在O点的磁感应强度方向水平向右 | |
| D. | 在O点的磁感应强度方向水平向左 |
15.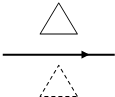 如图所示,一个闭合三角形导线框位于竖直平面内,其下方固定一根与线框所在的竖直平面平行且很靠近(但不重叠)的水平直导线,导线中通以图示方向的恒定电流.线框从实线位置由静止释放,在其后的运动过程中( )
如图所示,一个闭合三角形导线框位于竖直平面内,其下方固定一根与线框所在的竖直平面平行且很靠近(但不重叠)的水平直导线,导线中通以图示方向的恒定电流.线框从实线位置由静止释放,在其后的运动过程中( )
 如图所示,一个闭合三角形导线框位于竖直平面内,其下方固定一根与线框所在的竖直平面平行且很靠近(但不重叠)的水平直导线,导线中通以图示方向的恒定电流.线框从实线位置由静止释放,在其后的运动过程中( )
如图所示,一个闭合三角形导线框位于竖直平面内,其下方固定一根与线框所在的竖直平面平行且很靠近(但不重叠)的水平直导线,导线中通以图示方向的恒定电流.线框从实线位置由静止释放,在其后的运动过程中( )| A. | 线框受到安培力的合力方向竖直向上 | |
| B. | 线框中感应电流方向为先顺时针后逆时针 | |
| C. | 线框中的磁通量为零时其感应电流也为零 | |
| D. | 线框减少的重力势能全部转化为电能 |
12.用比值法定义物理量是物理学中一种很重要的思想方法,下列物理量由比值法定义正确的是( )
| A. | 加速度a=$\frac{F}{m}$ | B. | 磁感应强度B=$\frac{F}{IL}$ | C. | 电容C=$\frac{{?}_{r}S}{4πkd}$ | D. | 电流强度I=$\frac{U}{R}$ |
9.以下说法正确的是( )
| A. | 玻璃管的裂口烧熔后会变钝是表面张力的作用引起的 | |
| B. | 一种液体是否浸润某种固体,与这两种物质的性质都有关系 | |
| C. | 一切自然过程总是沿着分子热运动的无序性减小的方向进行 | |
| D. | 做油膜法估测分子直径的实验时,要先撒痱子粉再滴入酸酒精溶液 | |
| E. | 只要知道某种物质的摩尔体积和分子体积,就可以计算出阿伏加德罗常数 |
10. 如图所示,轻质弹簧一端固定在墙壁上,另一端与滑块A连接,滑块B与A接触而不粘连,两滑块质量均为m,桌面动摩擦因数为0.5,弹簧处于自然长度时滑块位于O点.现用水平向左的力将物块从O点推至P1点,OP1间距为L,推力做的功为3mgL(g为重力加速度),撤去推力两物块由静止向右运动,已知A向右运动的最远点为P2,之后A向左能运动到O点左侧的P3点(在P3速度瞬间为零之后又被弹回),则下列判断正确的有( )
如图所示,轻质弹簧一端固定在墙壁上,另一端与滑块A连接,滑块B与A接触而不粘连,两滑块质量均为m,桌面动摩擦因数为0.5,弹簧处于自然长度时滑块位于O点.现用水平向左的力将物块从O点推至P1点,OP1间距为L,推力做的功为3mgL(g为重力加速度),撤去推力两物块由静止向右运动,已知A向右运动的最远点为P2,之后A向左能运动到O点左侧的P3点(在P3速度瞬间为零之后又被弹回),则下列判断正确的有( )
 如图所示,轻质弹簧一端固定在墙壁上,另一端与滑块A连接,滑块B与A接触而不粘连,两滑块质量均为m,桌面动摩擦因数为0.5,弹簧处于自然长度时滑块位于O点.现用水平向左的力将物块从O点推至P1点,OP1间距为L,推力做的功为3mgL(g为重力加速度),撤去推力两物块由静止向右运动,已知A向右运动的最远点为P2,之后A向左能运动到O点左侧的P3点(在P3速度瞬间为零之后又被弹回),则下列判断正确的有( )
如图所示,轻质弹簧一端固定在墙壁上,另一端与滑块A连接,滑块B与A接触而不粘连,两滑块质量均为m,桌面动摩擦因数为0.5,弹簧处于自然长度时滑块位于O点.现用水平向左的力将物块从O点推至P1点,OP1间距为L,推力做的功为3mgL(g为重力加速度),撤去推力两物块由静止向右运动,已知A向右运动的最远点为P2,之后A向左能运动到O点左侧的P3点(在P3速度瞬间为零之后又被弹回),则下列判断正确的有( )| A. | 两滑块向右运动过程中在弹簧恢复原长时分离 | |
| B. | 两滑块一起向右运动过程中最大动能为mgL | |
| C. | 释放后,B向右运动的最远距离小于2L | |
| D. | 物块A从P2到P3的过程中,物块A动能最大时弹簧的弹性势能小于物块A在P3点时弹簧的弹性势能 |
