题目内容
7. 如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在水平面上向右运动.求小球从A点运动到地面所需的时间0.2s.(平面与斜面均光滑,取g=10m/s2).
如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在水平面上向右运动.求小球从A点运动到地面所需的时间0.2s.(平面与斜面均光滑,取g=10m/s2).
分析 首先讨论小球离开斜面做平抛运动,是落在斜面上还是落在地面上,然后运动学规律求解.
解答 解:由于小球开始在水平面上运动,离开A点时小球将做平抛运动,而不会沿斜面下滑,在运动到地面之前小球是否经历斜面,要看以下条件:小球平抛到地面的水平距离为s=${v}_{0}t={v}_{0}\sqrt{\frac{2h}{g}}=5×\sqrt{\frac{2×0.2}{10}}s=1m$,
斜面底宽d=$hcotθ=0.2×\sqrt{3}m$=0.35m,
因为s>d,所以小球离开A点后不会落到斜面上.
因此落地时间即为平抛运动所需的时间.
t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.2}{10}}s=0.2s$.
故答案为:0.2s.
点评 解决本题的关键知道平抛运动在水平方向做匀速直线运动,在竖直方向上自由落体运动.掌握平抛运动的运动学规律.

练习册系列答案
相关题目
18. 如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.现让小球在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,则小球在最高点的速度V满足( )
如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.现让小球在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,则小球在最高点的速度V满足( )
 如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.现让小球在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,则小球在最高点的速度V满足( )
如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.现让小球在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,则小球在最高点的速度V满足( )| A. | 0≤V≤$\sqrt{gr}$ | B. | $\sqrt{gr}$≤V≤$\sqrt{2gr}$ | C. | $\sqrt{gr}$≤V≤$\sqrt{3gr}$ | D. | $\sqrt{2gr}$≤V≤$\sqrt{3gr}$ |
15.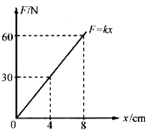 一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
 一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )| A. | 3.6J,-3.6J | B. | -3.6J,3.6J | C. | 1.8J,-1.8J | D. | -1.8J,1.8J |
2.中国有亚洲最大的潜艇部队,拥有自行开发的宋级柴电动力潜艇和汉级核动力潜艇,核动力潜艇中核反应堆释放的核能被转化成动能和电能.核反应堆的工作原理是利用中子轰击重核发生裂变反应,释放出大量的核能.核反应方程${\;}_{92}^{235}$U+n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+αX是反应堆中发生的众多核反应的一种,n为中子,X为待求粒子,α为X的个数,则( )
| A. | X为质子 α=3 | B. | X为质子 α=2 | C. | X为中子 α=2 | D. | X为中子 α=3 |
12.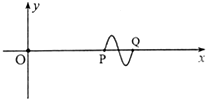 O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
 O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )| A. | 第一列波的起振方向向上 | B. | 第一列波的传播周期为0.1s | ||
| C. | 两列波的传播速度相同 | D. | 第二列波的传播周期是0.8s |
13. 如图所示是点电荷Q周围的一条水平向右的电场线,P是这条电场线上的一点,则以下判断正确的是( )
如图所示是点电荷Q周围的一条水平向右的电场线,P是这条电场线上的一点,则以下判断正确的是( )
 如图所示是点电荷Q周围的一条水平向右的电场线,P是这条电场线上的一点,则以下判断正确的是( )
如图所示是点电荷Q周围的一条水平向右的电场线,P是这条电场线上的一点,则以下判断正确的是( )| A. | Q是正电荷,P点的场强方向水平向右 | |
| B. | Q是正电荷,P点的场强方向水平向左 | |
| C. | Q是负电荷,P点的场强方向水平向右 | |
| D. | Q是负电荷,P点的场强方向水平向左 |